LPCC (Linear Prediction Cepstral Coefficients): Fundamentos, Algoritmos e Aplicações em Sistemas Embarcados

1 — LPC (Linear Predictive Coding)

O que significa LPC

LPC é o acrônimo de Linear Predictive Coding (Codificação Preditiva Linear).
Trata-se de um método matemático usado para modelar sinais, especialmente sinais de fala e áudio, assumindo que cada amostra do sinal pode ser aproximada como uma combinação linear de amostras passadas.

Em termos simples:

o LPC tenta responder à pergunta
“Dado o passado recente do sinal, qual é o melhor valor para a próxima amostra?”

Essa ideia é central em processamento de fala, reconhecimento de padrões acústicos e, mais recentemente, em pipelines de extração de características cepstrais, como o LPCC.

Intuição física e de sinal

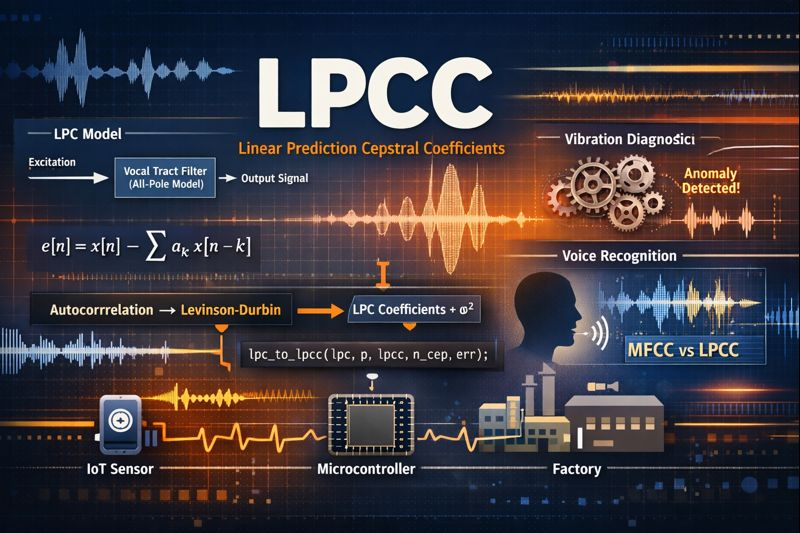
No contexto de fala (mas não limitado a ele), o LPC modela o sinal como:

• Uma fonte de excitação (ex.: vibração das cordas vocais)
• Um filtro linear (trato vocal, cavidade acústica, ou sistema ressonante)

Matematicamente, o sinal é tratado como a saída de um filtro tudo-polo (all-pole) excitado por um sinal simples.

Isso é importante porque:

• Formantes (ressonâncias) aparecem naturalmente nos polos do modelo
• O modelo é compacto, computacionalmente eficiente e estável

Modelo matemático do LPC

O sinal discreto ( x[n] ) é modelado como:

\[
x[n] = -\sum_{k=1}^{p} a_k , x[n-k] + e[n]
\]

onde:

• \( a_k \) → coeficientes LPC
• \( p \) → ordem do modelo
• \( e[n] \) → erro de predição (resíduo)

O objetivo do LPC é escolher os coeficientes \( a_k \) que minimizam a energia média do erro.

Isso leva diretamente às Equações de Yule-Walker, resolvidas normalmente pelo algoritmo de Levinson-Durbin — que veremos em código C mais à frente.

Por que o LPC é importante para LPCC

Aqui está o ponto-chave que conecta esta seção ao restante do artigo:

• LPCC (Linear Prediction Cepstral Coefficients) não existem sem LPC
• O LPC fornece:
  • Os coeficientes do filtro
  • A estrutura espectral
• O LPCC transforma esses coeficientes em um domínio cepstral, mais adequado para:
  • Reconhecimento de padrões
  • Classificação
  • Machine Learning clássico

Ou seja:

LPC modela o sistema
LPCC descreve o sistema

Implementação conceitual do LPC em C (visão geral)

Antes do código completo, o pipeline típico em C é:

1. Janela do sinal (ex.: Hamming)
2. Cálculo da autocorrelação
3. Levinson-Durbin → coeficientes LPC
4. Conversão LPC → LPCC (próxima seção futura)

Nesta seção, focamos apenas no LPC puro.

Exemplo em C — cálculo da autocorrelação

#include <stddef.h>

/**
 * Calcula a autocorrelação de um sinal
 * x      : sinal de entrada
 * N      : número de amostras
 * p      : ordem LPC
 * r      : vetor de autocorrelação (tamanho p+1)
 */
void autocorrelation(const float *x, size_t N, size_t p, float *r)
{
    for (size_t k = 0; k <= p; k++) {
        r[k] = 0.0f;
        for (size_t n = k; n < N; n++) {
            r[k] += x[n] * x[n - k];
        }
    }
}

#include <stddef.h>

/**
 * Calcula a autocorrelação de um sinal
 * x      : sinal de entrada
 * N      : número de amostras
 * p      : ordem LPC
 * r      : vetor de autocorrelação (tamanho p+1)
 */
void autocorrelation(const float *x, size_t N, size_t p, float *r)
{
    for (size_t k = 0; k <= p; k++) {
        r[k] = 0.0f;
        for (size_t n = k; n < N; n++) {
            r[k] += x[n] * x[n - k];
        }
    }
}

Esse vetor r[k] é exatamente o que alimenta o algoritmo de Levinson-Durbin, que gera os coeficientes LPC.

Observações práticas para sistemas embarcados

Do ponto de vista de firmware e IoT:

• LPC é extremamente viável em microcontroladores
• Complexidade: ( O(p^2) )
• Pode ser executado:
  • Em tempo real
  • Com DMA + buffers circulares
  • Integrado a pipelines FreeRTOS ou Zephyr

Isso explica por que LPC/LPCC ainda são relevantes mesmo em tempos de deep learning.