Introdução
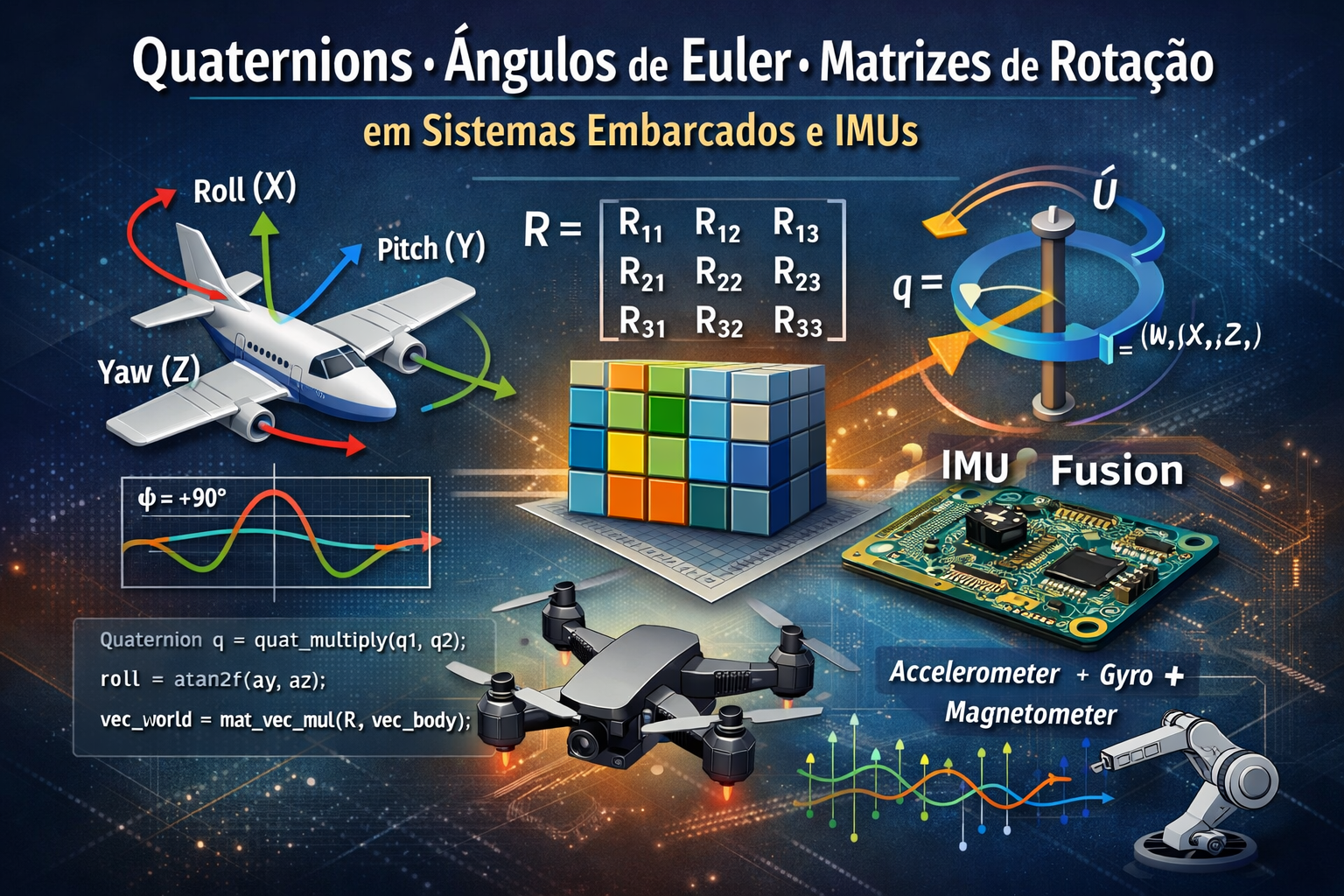
Quando você coloca uma IMU (Unidade de Medição Inercial) como MPU6050, MPU9250 ou qualquer combinação de acelerômetro e giroscópio dentro de um projeto embarcado, você acaba esbarrando cedo ou tarde na mesma pergunta: “como eu represento a orientação do meu objeto no espaço de um jeito que eu consiga calcular inclinação, compensar gravidade, integrar rotações ao longo do tempo e ainda não destruir a estabilidade numérica do firmware?”. É aí que entram três famílias de representações que parecem concorrentes, mas na prática se complementam: ângulos de Euler (roll, pitch, yaw), vetores de orientação (por exemplo, matriz de rotação ou pares de vetores base do corpo) e quaternions.
Ângulos de Euler são intuitivos e ótimos para interfaces humanas: “inclinei 10° para frente”, “girei 30° no eixo Z”. O problema é que eles carregam armadilhas matemáticas quando você precisa acumular rotações ou passar por certas combinações de ângulos, especialmente o famoso gimbal lock (perda de um grau de liberdade). Vetores de orientação e matrizes de rotação são muito diretos do ponto de vista geométrico: você literalmente descreve para onde apontam os eixos do corpo no referencial do mundo, e isso é excelente para transformar vetores (como gravidade, aceleração e magnetismo) entre referenciais; em contrapartida, matrizes exigem mais operações, precisam ser re-ortogonalizadas para não “entortar” com erro numérico e ocupam mais memória.
Quaternions entram como uma representação que, apesar de menos intuitiva à primeira vista, é extremamente eficiente e robusta para integrar rotações com giroscópio, evitar gimbal lock e manter estabilidade numérica com um custo computacional baixo o suficiente para microcontroladores. Na prática, muita gente usa quaternions “por dentro” do filtro (Madgwick, Mahony, EKF etc.) e converte para Euler “por fora” quando precisa exibir ângulos ou configurar limites.
Nas próximas seções, eu vou construir esse entendimento em camadas: primeiro ângulos de Euler e suas relações trigonométricas, depois vetores/matrizes de orientação (com a leitura geométrica do que está acontecendo), e em seguida quaternions, mostrando como eles representam rotação, como compor rotações e como converter entre as formas. Em cada conceito eu vou demonstrar em C, com código comentado, como: (1) representar a orientação, (2) atualizar essa orientação com incrementos de rotação, e (3) extrair ângulos e também aplicar a orientação para separar aceleração linear da gravidade (o passo que faz “movimento” ficar mensurável a partir do acelerômetro).