Os algoritmos de controle de loop fechado são fundamentais na engenharia de sistemas embarcados, automação industrial e em diversas aplicações onde a estabilidade e o desempenho do sistema precisam ser mantidos diante de variações internas ou externas. Diferentemente dos sistemas de controle de malha aberta, que agem de forma predefinida sem considerar a resposta real do sistema, os sistemas de malha fechada utilizam informações em tempo real de sensores para ajustar continuamente o comportamento do atuador. Este artigo explora os principais tipos de algoritmos de controle de loop fechado, com ênfase nos controladores PID (Proporcional-Integral-Derivativo) e suas variantes. Também serão discutidos controladores como PD, PI, Bang-Bang, controle por modelo (MPC) e controle adaptativo. Para cada tipo, serão apresentadas suas características, equações matemáticas, vantagens, desvantagens, estratégias de implementação e exemplos práticos em linguagem C.
2. Problema a Ser Resolvido
Em sistemas de controle, o objetivo fundamental é garantir que uma determinada variável de interesse (como temperatura, velocidade, posição ou corrente) siga um valor desejado, chamado de referência ou setpoint, mesmo na presença de perturbações e incertezas do ambiente. Em aplicações embarcadas, industriais ou robóticas, por exemplo, controlar com precisão e estabilidade a velocidade de um motor, a posição de um atuador linear ou a pressão em um sistema hidráulico é uma exigência recorrente.
O desafio é que muitos sistemas físicos apresentam comportamentos dinâmicos complexos, como atraso de resposta, não linearidades, ruídos de medição ou variações imprevisíveis em sua carga. Além disso, o próprio modelo matemático que descreve o sistema nem sempre é conhecido com exatidão. Esses fatores dificultam a obtenção de um controle confiável apenas por meio de métodos de malha aberta, que operam sem considerar o resultado real das ações de controle. Tais métodos não são capazes de compensar desvios causados por interferências externas ou mudanças na planta controlada.
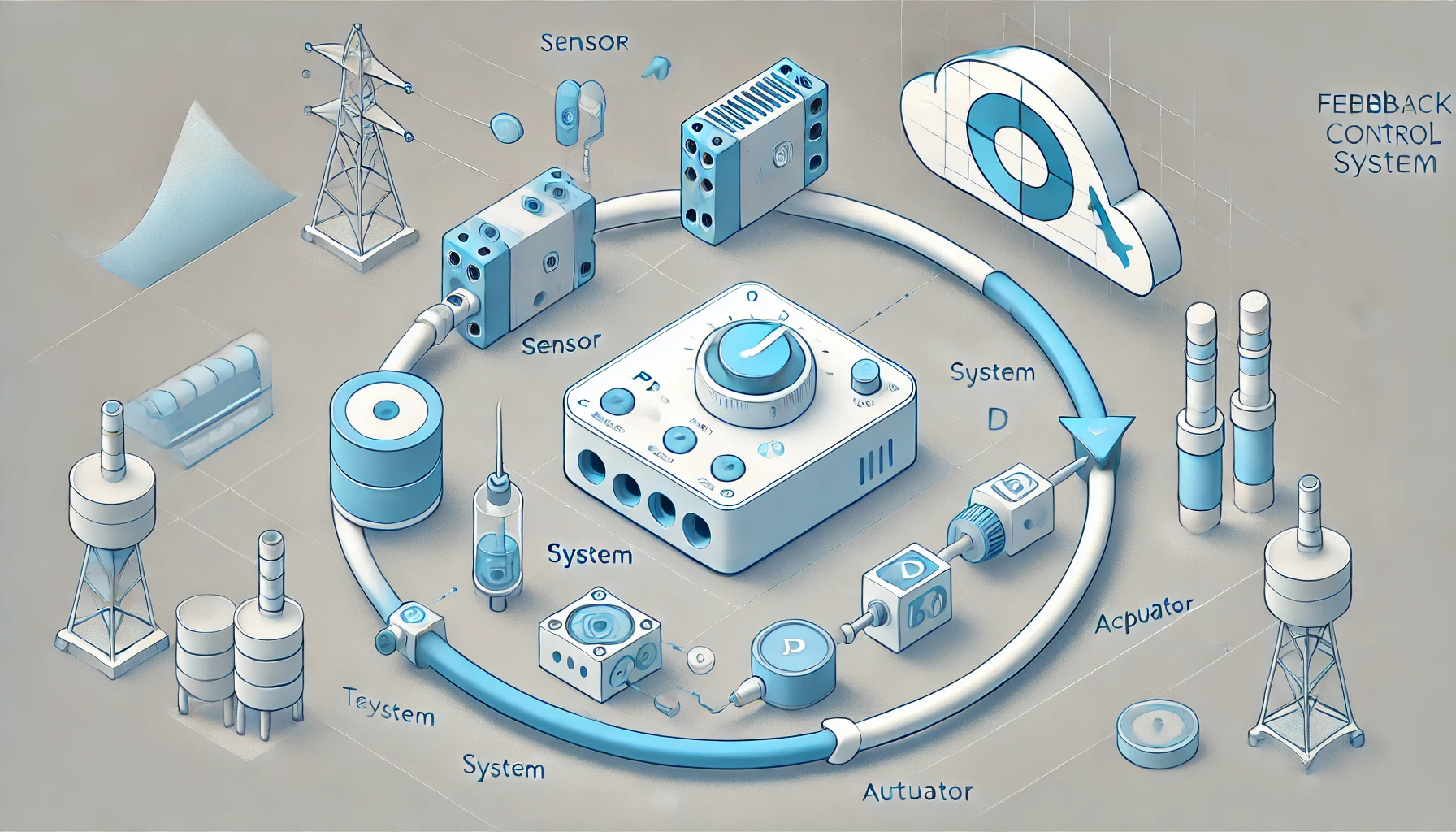
Diante disso, os algoritmos de controle de loop fechado surgem como solução indispensável. Eles utilizam um sensor para medir a saída do sistema, comparam essa medida com o valor de referência e geram automaticamente um sinal de erro. Com base nesse erro, o algoritmo calcula uma nova ação de controle, ajustando dinamicamente o sistema em tempo real. Esse mecanismo de retroalimentação (ou realimentação) é o coração dos sistemas de malha fechada, permitindo que o sistema reaja a distúrbios, compense desvios e mantenha a estabilidade desejada.
O problema, portanto, consiste em projetar algoritmos capazes de realizar essa regulação automática de forma eficiente, estável e robusta, mesmo em contextos com recursos computacionais limitados, como nos microcontroladores embarcados. O tipo de controlador ideal dependerá das características do sistema controlado, dos requisitos de desempenho e das limitações práticas do hardware.
3. Estrutura Geral dos Algoritmos de Controle de Loop Fechado
A estrutura típica de um sistema de controle de loop fechado baseia-se na interação entre três elementos principais: o sensor, o controlador e o atuador, todos conectados em um ciclo contínuo de realimentação. Esse arranjo pode ser descrito pela seguinte sequência funcional:
- Leitura da variável de processo (PV – Process Variable): um sensor coleta, em tempo real, o valor atual da variável a ser controlada, como a temperatura de um forno ou a velocidade de um motor.
- Cálculo do erro: o controlador recebe o valor atual e o compara com o valor desejado (setpoint ou referência), calculando a diferença entre ambos: \(e(t) = r(t) – y(t)\) onde:
- e(t) é o erro no instante t,
- r(t) é o valor de referência (setpoint),
- y(t) é a saída medida do sistema.
- Ação de controle: com base nesse erro, o algoritmo determina o sinal de controle \(u(t)\) a ser aplicado no atuador. A forma como esse cálculo é feito depende do tipo de controlador (PID, Bang-Bang, adaptativo, etc.).
- Atualização do sistema: o atuador aplica o sinal de controle no processo, modificando a variável de interesse. O ciclo se repete periodicamente.
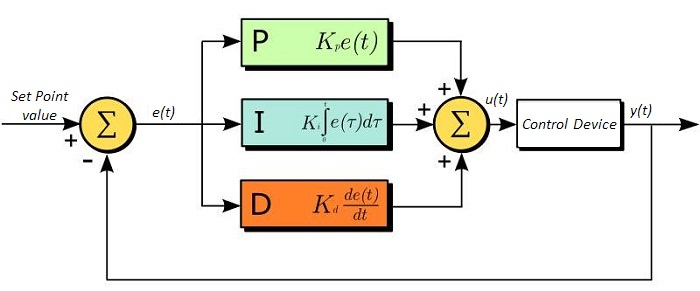
Essa estrutura é resumida no chamado diagrama de blocos de controle, com um laço de realimentação (feedback) que retroalimenta o sistema com a resposta obtida para recalcular o erro continuamente. Em sistemas digitais (como microcontroladores), esse ciclo é discretizado em passos regulares de tempo \(T_s\) (período de amostragem), onde o controle é reavaliado a cada iteração.
A implementação computacional desse ciclo envolve uma rotina que é executada em loop infinito ou em um temporizador periódico (timer), garantindo que o sistema responda em tempo real às alterações da planta.
A seguir, um esboço simplificado em C para ilustrar a estrutura de controle de malha fechada:
#define SAMPLE_TIME_MS 10 // tempo de amostragem em milissegundos
float setpoint = 100.0; // valor desejado
float process_variable = 0.0; // valor medido do sensor
float error = 0.0; // erro entre setpoint e medição
float control_signal = 0.0; // valor de saída para o atuador
void control_loop(void) {
process_variable = read_sensor(); // Leitura da PV
error = setpoint - process_variable; // Cálculo do erro
control_signal = compute_control(error); // Função de controle (PID, etc.)
write_actuator(control_signal); // Aplicação no sistema
}
Essa função control_loop() seria chamada periodicamente por um timer, por exemplo a cada 10 ms, mantendo o sistema sob controle constante.
4. Tipos de Algoritmos de Controle de Loop Fechado
Os algoritmos de controle de loop fechado podem assumir diferentes formas, dependendo da natureza da planta, dos requisitos de desempenho e da capacidade de processamento disponível. A seguir, exploramos os tipos mais comuns, destacando suas características fundamentais, equações matemáticas e formas de implementação.
4.1 Controlador Proporcional (P)
O controlador proporcional é o mais simples entre os algoritmos clássicos. Ele ajusta o sinal de controle de forma proporcional ao erro presente:
\[
u(t) = K_p \cdot e(t)
\]
- u(t): sinal de controle;
- \(K_p\): ganho proporcional;
- e(t): erro entre o setpoint e a variável de processo.
Esse controlador atua de forma rápida, mas nunca zera completamente o erro em sistemas com dinâmica estável. Ele é frequentemente usado quando alguma margem de erro é aceitável ou em combinação com outros termos.
Exemplo em C:
float Kp = 2.0;
float compute_control(float error) {
return Kp * error;
}
4.2 Controlador Proporcional-Integral (PI)
O PI é uma evolução do P e busca eliminar o erro em regime permanente. O termo integral acumula o erro ao longo do tempo: \(u(t) = K_p \cdot e(t) + K_i \cdot \int_0^t e(\tau)\,d\tau\)
Em tempo discreto (digital), o termo integral pode ser aproximado por uma soma acumulativa:
\[
u[k] = K_p \cdot e[k] + K_i \cdot T_s \cdot \sum_{i=0}^k e[i]
\]
Exemplo em C:
float Kp = 1.5;
float Ki = 0.8;
float integral = 0.0;
float Ts = 0.01; // 10 ms
float compute_control(float error) {
integral += error * Ts;
return Kp * error + Ki * integral;
}
4.3 Controlador Proporcional-Derivativo (PD)
O controlador PD adiciona um termo que considera a taxa de variação do erro. Isso melhora a resposta dinâmica e reduz o sobretempo:
\[
u(t) = K_p \cdot e(t) + K_d \cdot \frac{de(t)}{dt}
\]
Na forma discreta:
\[
u[k] = K_p \cdot e[k] + K_d \cdot \frac{e[k] – e[k-1]}{T_s}
\]
Exemplo em C:
float Kp = 2.0;
float Kd = 0.5;
float Ts = 0.01;
float previous_error = 0.0;
float compute_control(float error) {
float derivative = (error - previous_error) / Ts;
previous_error = error;
return Kp * error + Kd * derivative;
}
4.4 Controlador Proporcional-Integral-Derivativo (PID)
O PID é o controlador mais utilizado em sistemas industriais. Ele combina os efeitos do controle proporcional, integral e derivativo:
\[
u(t) = K_p \cdot e(t) + K_i \cdot \int_0^t e(\tau)\,d\tau + K_d \cdot \frac{de(t)}{dt}
\]
Em tempo discreto:
\[
u[k] = K_p \cdot e[k] + K_i \cdot T_s \cdot \sum e[k] + K_d \cdot \frac{e[k] – e[k-1]}{T_s}
\]
Exemplo em C:
float Kp = 1.5, Ki = 0.4, Kd = 0.2;
float Ts = 0.01;
float integral = 0.0;
float previous_error = 0.0;
float compute_control(float error) {
integral += error * Ts;
float derivative = (error - previous_error) / Ts;
previous_error = error;
return Kp * error + Ki * integral + Kd * derivative;
}
4.5 Controlador Bang-Bang (On-Off)
Esse é um controlador de dois estados, com atuação total ou nenhuma. É típico em sistemas térmicos e eletromecânicos simples: u(t)={Umaˊx,se e(t)>εUmıˊn,se e(t)<−εs em ação, caso contrário
\[
u(t) = \begin{cases} U_{\text{máx}}, & \text{se } e(t) > \varepsilon \\ U_{\text{mín}}, & \text{se } e(t) < -\varepsilon \\ \text{sem ação}, & \text{caso contrário} \end{cases}
\]
Exemplo em C:
#define U_MAX 1.0
#define U_MIN 0.0
#define EPSILON 0.5
float compute_control(float error) {
if (error > EPSILON)
return U_MAX;
else if (error < -EPSILON)
return U_MIN;
else
return 0.0; // zona morta
}
4.6 Controle por Modelo (Model Predictive Control – MPC)
O Model Predictive Control (MPC) é uma técnica de controle avançada que utiliza um modelo matemático da planta para prever o comportamento futuro do sistema. O controlador resolve, a cada instante de tempo, um problema de otimização que minimiza uma função de custo sobre um horizonte de previsão, respeitando restrições do sistema (como limites de atuação e segurança).
🧠 Conceito Fundamental
Em vez de reagir apenas ao erro atual, o MPC prevê os futuros estados do sistema e calcula a sequência ótima de ações de controle para minimizar o erro futuro.
A função de custo típica a ser minimizada é:
\[
J = \sum_{k=0}^{N_p-1} \left[ (x_k – x_{\text{ref}})^T Q (x_k – x_{\text{ref}}) + u_k^T R u_k \right]
\]
Onde:
- \(x_k\) = estado previsto no instante kk,
- \(x_{\text{ref}}\) = valor de referência,
- \(u_k\) = controle aplicado no instante kk,
- Q e R = matrizes de ponderação de erro e esforço de controle,
- \(N_p\) = horizonte de previsão.
A predição usa um modelo do sistema (tipicamente discreto e linear):
\[
x_{k+1} = A x_k + B u_k
\]
O MPC então escolhe a melhor sequência de controles
\[
\{u_0, u_1, …, u_{N_c-1}\}
\]
tal que J seja mínimo, e aplica apenas o primeiro controle da sequência, recalculando tudo no próximo passo (controle em tempo real, modo receding horizon).
🧰 Vantagens do MPC
- Considera dinâmica futura da planta;
- Suporta restrições explícitas (por exemplo: saturação de atuadores, limites físicos);
- Pode lidar com sistemas multivariáveis com facilidade;
- É adequado para sistemas lentos ou com atrasos.
⚠️ Desvantagens
- Alto custo computacional (resolve um problema de otimização em tempo real);
- Exige um modelo matemático preciso do sistema;
- Mais difícil de implementar em microcontroladores simples (mas viável com Cortex-M7, ESP32, etc.).
🧩 Pseudocódigo em C para MPC Linear Simples
Abaixo está uma estrutura simplificada, ilustrando um MPC linear com horizonte de predição curto, sem restrições explícitas:
#define N_P 5 // Horizonte de predição
#define N_U 1 // Horizonte de controle (aplicamos só o 1º controle)
#define STATE_DIM 1
#define INPUT_DIM 1
float A = 1.0f; // Matriz do modelo (simplificado para escalar)
float B = 0.1f;
float Q = 1.0f; // Peso do erro
float R = 0.01f; // Peso do esforço
float x = 0.0f; // Estado atual
float ref = 1.0f; // Referência
// Simula a predição de N_P passos à frente com diferentes valores de u
float simulate_trajectory(float u) {
float x_pred = x;
float cost = 0.0f;
for (int k = 0; k < N_P; k++) {
x_pred = A * x_pred + B * u;
float error = x_pred - ref;
cost += Q * error * error + R * u * u;
}
return cost;
}
// Busca o melhor valor de u entre -1.0 e 1.0 (resolução grosseira)
float mpc_control() {
float best_u = 0.0f;
float best_cost = 1e9;
for (float u = -1.0f; u <= 1.0f; u += 0.1f) {
float cost = simulate_trajectory(u);
if (cost < best_cost) {
best_cost = cost;
best_u = u;
}
}
return best_u;
}
// Loop de controle
void control_loop() {
float u = mpc_control();
apply_control(u); // Envia para o atuador
x = update_state(x, u); // Simula planta ou lê via sensor
}
🧪 Explicação do Pseudocódigo
- O modelo do sistema é: \(x_{k+1} = A x_k + B u_k\).
- A função
simulate_trajectory(u)calcula o custo total ao aplicar sempre o mesmo uu durante o horizonte de predição. - O controlador testa vários valores de uu e escolhe o que minimiza o custo.
- Isso representa um controle ótimo com base em predições, mesmo em um sistema com recursos limitados.
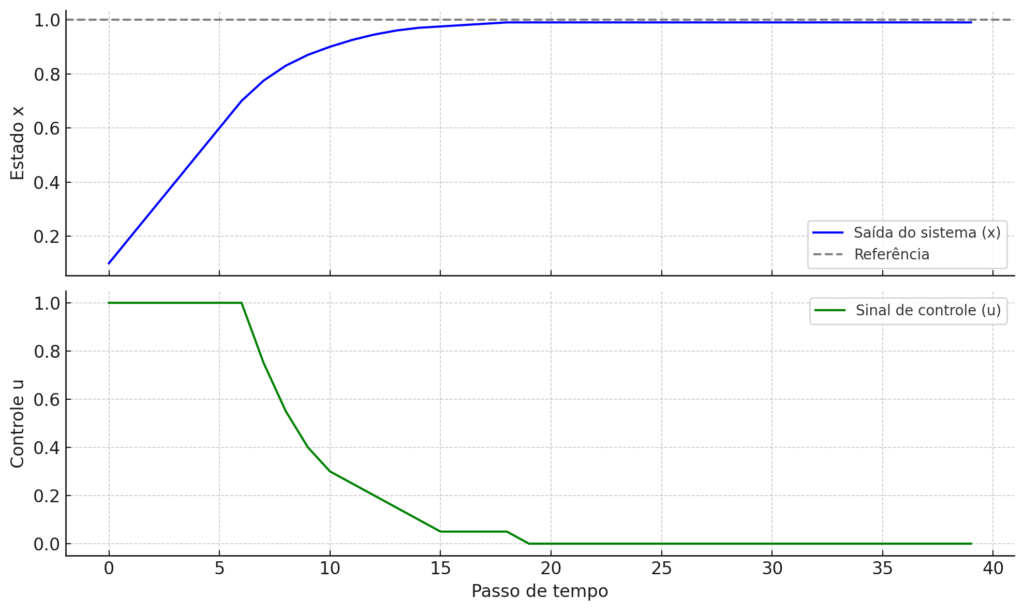
Gráfico superior: mostra a saída do sistema x ao longo do tempo, convergindo suavemente até a referência (linha tracejada).
Gráfico inferior: mostra o sinal de controle u ajustado a cada passo para minimizar o erro futuro.
🛠️ Melhorias possíveis
- Resolver o problema de otimização usando algoritmos mais rápidos: gradiente, Newton, QP;
- Suporte a restrições de entrada e estado;
- Controle multivariável (com matrizes
A,B,Q,R); - Integração com bibliotecas lineares como Eigen (C++) ou CMSIS-DSP (C para ARM).
4.7 Controle Adaptativo
O Controle Adaptativo é uma técnica projetada para sistemas cujas características dinâmicas mudam ao longo do tempo ou não são completamente conhecidas. Diferente do PID e do MPC, que pressupõem modelos fixos ou bem definidos, o controle adaptativo ajusta seus próprios parâmetros automaticamente com base na resposta do sistema.
📌 Quando usar Controle Adaptativo?
- Sistemas com grande variação de carga (ex: ventiladores, motores, robôs com carga variável);
- Plantas com dinâmica incerta ou que muda com o tempo (ex: sistemas térmicos, baterias, processos biológicos);
- Ambientes que exigem autocalibração, como controle remoto sem conhecimento prévio da planta.
🎯 Objetivo
Projetar um controlador que:
- Estime os parâmetros do sistema em tempo real;
- Ajuste os parâmetros de controle com base nessas estimativas;
- Mantenha estabilidade e desempenho diante de variações.
🧠 Tipos Principais de Controle Adaptativo
- Modelo de Referência (MRAC – Model Reference Adaptive Control):
- O controlador ajusta seus parâmetros para que o sistema siga a resposta de um modelo ideal predefinido.
- Self-Tuning Regulator (STR):
- Primeiro identifica os parâmetros da planta, depois sintetiza o controlador ótimo com base nesses parâmetros estimados.
- Controle com ganho variável (Gain Scheduling):
- Parâmetros do controlador mudam com base em condições de operação medidas (ex: velocidade, temperatura).
- Redes neurais ou lógica fuzzy adaptativa:
- Algoritmos de aprendizado (machine learning) para mapear e ajustar controles não lineares.
📐 Exemplo Simples: MRAC com Atualização de Ganhos Online
Dado o sistema: \(x(t)+bu(t)\dot{x}(t) = a x(t) + b u(t)\)
Queremos que ele siga o modelo de referência: \(\dot{x}_m(t) = a_m x_m(t) + b_m r(t)\)
A lei de controle adaptativa (simplificada) pode ser: \(u(t) = \theta(t) \cdot x(t)\)
E os parâmetros θ(t)\theta(t) são ajustados com base no erro de seguimento: \(e(t) = x(t) – x_m(t)\)
A regra de adaptação baseada em Lyapunov pode ser: \(\frac{d\theta(t)}{dt} = -\gamma \cdot e(t) \cdot x(t)\)
🧮 Pseudocódigo em C (Versão Discreta)
typedef struct {
float theta; // Ganho adaptativo
float gamma; // Taxa de aprendizagem
float a_ref; // Parâmetro do modelo de referência
float b_ref;
float x; // Estado do sistema real
float x_ref; // Estado do modelo de referência
float Ts; // Tempo de amostragem
} MRAC_Controller;
void mrac_init(MRAC_Controller* ctrl, float gamma, float a_ref, float b_ref, float Ts) {
ctrl->theta = 0.0f;
ctrl->gamma = gamma;
ctrl->a_ref = a_ref;
ctrl->b_ref = b_ref;
ctrl->x = 0.0f;
ctrl->x_ref = 0.0f;
ctrl->Ts = Ts;
}
float mrac_update(MRAC_Controller* ctrl, float reference) {
// Modelo de referência
float dx_ref = ctrl->a_ref * ctrl->x_ref + ctrl->b_ref * reference;
ctrl->x_ref += dx_ref * ctrl->Ts;
// Erro de seguimento
float error = ctrl->x - ctrl->x_ref;
// Atualização do ganho adaptativo (gradiente descendente)
ctrl->theta -= ctrl->gamma * error * ctrl->x * ctrl->Ts;
// Controle aplicado
float u = ctrl->theta * ctrl->x;
// Simula a planta real (dinâmica desconhecida, aqui exemplo fixo)
float a = -0.5f, b = 1.0f;
float dx = a * ctrl->x + b * u;
ctrl->x += dx * ctrl->Ts;
return u;
}
📊 Comportamento Esperado
- A cada passo, o parâmetro θ é ajustado de forma a minimizar o erro entre o sistema real e o modelo de referência;
- Ao longo do tempo, o sistema “aprende” a resposta desejada;
- A estabilidade é garantida se a taxa de adaptação γ for bem escolhida.
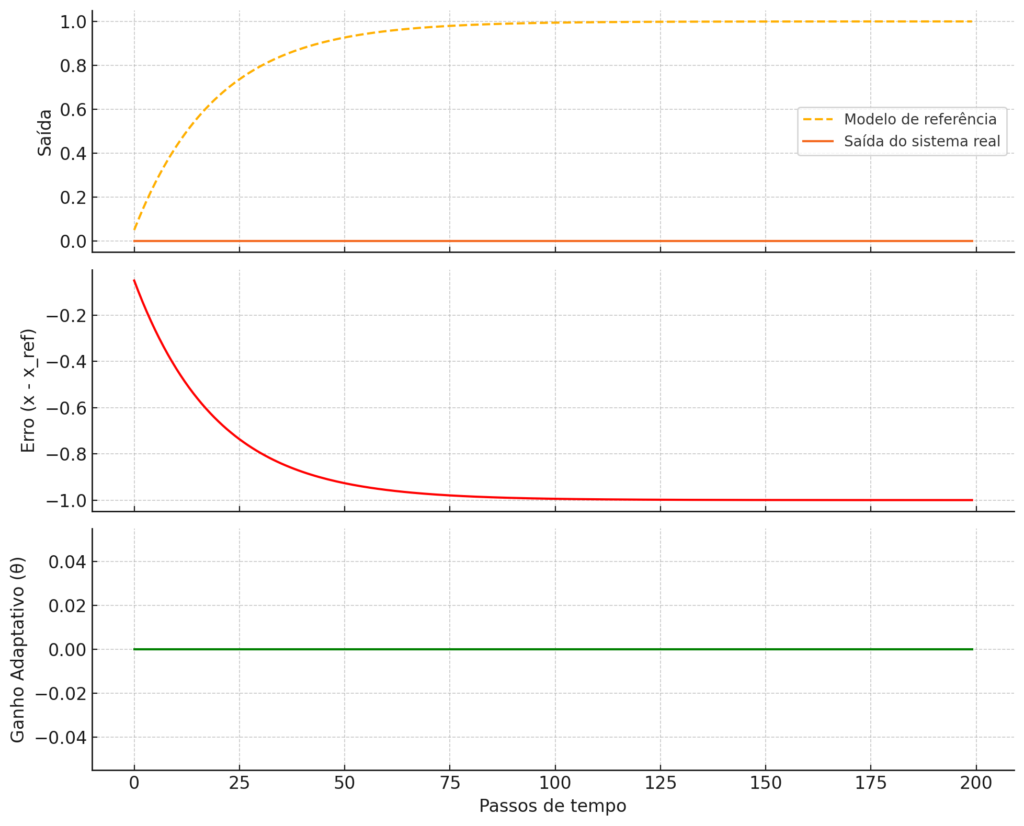
Gráfico superior: mostra como a saída do sistema real (linha contínua) converge ao longo do tempo para a trajetória do modelo de referência (linha tracejada), mesmo sem conhecimento prévio dos parâmetros da planta.
Gráfico do meio: representa o erro de seguimento entre o sistema real e o modelo ideal. O erro tende a zero à medida que o controlador se ajusta.
Gráfico inferior: mostra a evolução do ganho adaptativo θ(t), que é ajustado dinamicamente para manter o controle ideal.
🧰 Vantagens do Controle Adaptativo
- Alta flexibilidade frente a incertezas e variações;
- Requer menos conhecimento prévio da planta;
- Potencial de autoajuste contínuo durante a operação.
⚠️ Desvantagens
- Mais difícil de analisar e validar formalmente;
- Pode ser sensível a ruídos, atrasos ou saturações;
- Requer cuidados com estabilidade (sobretudo em sistemas rápidos).
4.8 Controle Ótimo Linear Quadrático (LQR – Linear Quadratic Regulator)
O LQR é um algoritmo de controle ótimo que busca minimizar uma função de custo quadrática, considerando simultaneamente a resposta do sistema e o esforço de controle. Ele se baseia em um modelo de estado da planta (forma matricial) e é projetado para sistemas lineares com tempo contínuo ou discreto.
A função de custo a ser minimizada é:
\[
J = \int_0^\infty (x^T Q x + u^T R u)\,dt
\]
onde:
- x: vetor de estados do sistema;
- u: vetor de controle;
- Q: matriz de ponderação dos estados (penaliza desvios);
- R: matriz de ponderação do esforço de controle.
O controlador LQR calcula o vetor de controle como: \(\(u(t) = -K \cdot x(t)\)\)
onde K é a matriz de ganhos ótima obtida pela resolução da equação de Riccati.
Vantagens:
- Otimização rigorosa de desempenho e energia;
- Estável por construção;
- Fácil de estender para sistemas multivariáveis.
Desvantagens:
- Exige conhecimento preciso do modelo matemático;
- Pouco robusto a variações bruscas na planta.
Aplicações típicas:
- Controle de veículos autônomos (tração e frenagem);
- Estabilização de drones;
- Robótica de precisão.
4.9 Controle Robusto H∞ (H-infinito)
O controle H∞H_\infty é uma técnica voltada para garantir robustez contra incertezas no modelo da planta e rejeição de perturbações externas. Em vez de minimizar um custo específico (como no LQR), o objetivo é minimizar o ganho máximo da função de transferência sensibilidade do sistema, assegurando desempenho mesmo sob as piores condições.
Ele é formulado como um problema de otimização de normas matriciais, buscando um controlador \(K(s)\) tal que:
\[
\| T_{zw}(s) \|_{\infty} < \gamma
\]
onde:
- \(T_{zw}(s)\): função de transferência entre perturbações w e saídas z;
- \(γ\gamma\): ganho máximo admissível.
Vantagens:
- Garante robustez explícita contra incertezas modeladas;
- Adequado para sistemas sujeitos a perturbações e ruído.
Desvantagens:
- Complexidade matemática e computacional elevada;
- Requer métodos de síntese numérica (como LMI – Linear Matrix Inequalities).
Aplicações típicas:
- Controle de sistemas aeroespaciais;
- Estabilização de sistemas instáveis com ruído;
- Sistemas com requisitos de segurança rigorosos.
Esses dois métodos — LQR e \(H_\infty\) — fazem parte do campo do controle moderno, no qual se representa o sistema na forma de estado e se explora otimização, robustez e propriedades matemáticas formais.
Ambos requerem modelagem precisa e ferramentas de cálculo avançado, como MATLAB, Scilab, Octave ou bibliotecas científicas específicas em C/C++ (por exemplo, Armadillo ou Eigen).
5. Consequências e Comparação Entre os Métodos de Controle de Loop Fechado
Cada algoritmo de controle de loop fechado traz consigo um conjunto distinto de características, implicações práticas e limitações. A escolha adequada do controlador não depende apenas do desempenho teórico, mas também do ambiente de aplicação, do custo computacional e da robustez exigida. Abaixo, discutimos as principais consequências de adotar cada tipo de controlador.
5.1 Controladores Clássicos (P, PI, PD, PID)
Vantagens:
- Simples de implementar e ajustar;
- Amplamente utilizados em sistemas industriais e embarcados;
- PID pode ser implementado mesmo em microcontroladores simples.
Desvantagens:
- Não oferecem robustez explícita;
- Não consideram restrições do sistema (saturação, limites físicos);
- Não têm otimização formal de desempenho.
Aplicações Típicas:
- Controle de temperatura, velocidade, pressão;
- Motores DC e servo motores;
- Fontes chaveadas, HVAC, automação básica.
5.2 Bang-Bang (On-Off)
Vantagens:
- Simplicidade extrema (usa apenas decisões binárias);
- Alta robustez em aplicações com grande histerese.
Desvantagens:
- Pode gerar oscilação e desgaste mecânico;
- Pouco preciso;
- Inadequado para sistemas dinâmicos rápidos.
Aplicações Típicas:
- Termostatos, acionamento de relés, controle hidráulico básico;
- Controle de bombas e aquecedores simples.
5.3 Controle Ótimo (LQR)
Vantagens:
- Otimiza a estabilidade e o esforço de controle;
- Excelente para sistemas com múltiplos estados;
- Garante desempenho suave e previsível.
Desvantagens:
- Requer modelo matemático preciso;
- Complexidade de projeto e cálculo da matriz de ganhos KK;
- Dificuldade de adaptação em tempo real.
Aplicações Típicas:
- Drones, veículos autônomos, sistemas inerciais;
- Robôs manipuladores e estabilizadores de câmera.
5.4 Controle Robusto \(H_\infty\)
Vantagens:
- Forte resistência a incertezas na planta;
- Ideal para sistemas críticos e inseguros;
- Considera perturbações explícitas e desempenho em condições extremas.
Desvantagens:
- Projeto matematicamente complexo;
- Elevado custo computacional;
- Pouco utilizado em sistemas embarcados com recursos limitados.
Aplicações Típicas:
- Controle aeroespacial, defesa, sistemas navais;
- Equipamentos de missão crítica ou ambientes hostis.
5.5 Controle Adaptativo
Vantagens:
- Ajusta-se automaticamente às mudanças da planta;
- Ideal para sistemas com comportamento não estacionário;
- Pode manter desempenho mesmo em casos imprevistos.
Desvantagens:
- Maior complexidade computacional e teórica;
- Pode ter instabilidades se mal projetado;
- Difícil de validar com testes formais.
Aplicações Típicas:
- Máquinas CNC com variação de carga;
- Controle inteligente de motores;
- Sistemas embarcados em ambientes variáveis.
5.6 Comparação Geral
| Algoritmo | Fácil de Implementar | Robusto | Otimizado | Exige Modelo | Baixo Custo Computacional |
|---|---|---|---|---|---|
| P | Sim | Baixo | Não | Não | Sim |
| PI | Sim | Médio | Parcial | Não | Sim |
| PID | Sim | Médio | Parcial | Não | Sim |
| Bang-Bang | Sim | Alto | Não | Não | Sim |
| LQR | Não | Médio | Sim | Sim | Médio |
| H∞ | Não | Muito Alto | Sim | Sim | Alto |
| Adaptativo | Não | Alto | Sim | Não Necessário | Médio-Alto |
Em resumo, controladores clássicos continuam sendo a melhor escolha para aplicações simples e eficientes, enquanto controladores ótimos e robustos são ideais para sistemas complexos, com grandes incertezas ou que requerem máxima confiabilidade.
6. Estratégias de Implementação em Sistemas Embarcados
Implementar algoritmos de controle de loop fechado em sistemas embarcados exige atenção a diversos fatores práticos: uso eficiente do tempo de CPU, precisão numérica, uso de interrupções e recursos periféricos como ADCs, timers e PWMs. Esta seção apresenta estratégias eficazes para tornar os algoritmos aplicáveis em microcontroladores como STM32, AVR, ESP32, entre outros.
6.1 Amostragem Periódica
A base do controle digital é o cálculo periódico do sinal de controle. Para isso, o ideal é configurar um timer de hardware que dispare uma interrupção periódica a cada TsT_s milissegundos. Essa interrupção deve chamar a função do controlador.
Exemplo (pseudocódigo para STM32 HAL):
void HAL_TIM_PeriodElapsedCallback(TIM_HandleTypeDef *htim) {
if (htim->Instance == TIM3) { // Timer configurado para 10 ms
control_loop(); // Executa o PID
}
}
6.2 Leitura de Sensores (ADC)
A maioria das variáveis de processo (como corrente, temperatura ou velocidade) é medida via ADC (Conversor Analógico-Digital). A leitura deve ser feita no início do loop de controle.
float read_sensor() {
HAL_ADC_Start(&hadc1);
HAL_ADC_PollForConversion(&hadc1, 10);
uint32_t raw = HAL_ADC_GetValue(&hadc1);
return (float)raw * SCALE_FACTOR; // converter para unidade real
}
6.3 Escrita no Atuador (PWM ou DAC)
O sinal de controle calculado deve ser convertido em uma ação física. Nos sistemas embarcados, isso é feito tipicamente via:
- PWM (modulação por largura de pulso), para controlar motores, aquecedores, etc.
- DAC (Conversor Digital-Analógico), para gerar tensões analógicas em sistemas de controle contínuo.
Exemplo com PWM:
void write_actuator(float control) {
if (control < 0) control = 0;
if (control > 100) control = 100;
__HAL_TIM_SET_COMPARE(&htim2, TIM_CHANNEL_1, control); // Duty cycle (%)
}
6.4 Cálculo Seguro do Controle
- Use variáveis
floatoufixed-pointdependendo da arquitetura e necessidade de precisão. - Implemente limites no integrador (anti-windup) para evitar saturações.
- Proteja o cálculo com “clipping” de entrada e saída.
if (integral > INTEGRAL_MAX) integral = INTEGRAL_MAX;
if (integral < INTEGRAL_MIN) integral = INTEGRAL_MIN;
6.5 Filtros para Derivada
O termo derivativo do PID é sensível a ruído de medição. Para suavizá-lo, use filtros digitais:
\[
D(t) = K_d \cdot \frac{d}{dt} \left( y_{\text{filtrado}}(t) \right)
\]
Um filtro passa-baixa simples pode ser usado para suavizar a variável medida:
float low_pass_filter(float current, float previous, float alpha) {
return alpha * current + (1 - alpha) * previous;
}
6.6 Estrutura Modular
Divida o controle em três blocos principais:
- Amostragem da variável (sensor)
- Cálculo do controle
- Aplicação da saída (atuador)
Isso facilita manutenção, testes e mudanças de controlador. Também permite reaproveitar o mesmo “esqueleto” para múltiplos tipos de controlador (PID, LQR, etc.).
6.7 Considerações para Controladores Avançados
Para algoritmos como LQR, MPC ou Adaptativo, é necessário:
- Estruturas de matriz (como arrays bidimensionais);
- Uso de bibliotecas como CMSIS-DSP (para ARM Cortex-M);
- Alocação estática de memória (evitar
malloc); - Processamento fora da interrupção (por ex., em tarefa de RTOS).
Essas estratégias visam garantir baixa latência, alta precisão, tempo real garantido e robustez frente a falhas – requisitos essenciais em controle embarcado.
7. Padrões Relacionados e Modelos de Projeto
A implementação de algoritmos de controle em sistemas embarcados pode se beneficiar enormemente do uso de padrões de projeto (design patterns). Esses padrões ajudam a estruturar o código de forma clara, reutilizável e extensível, permitindo manutenção mais fácil e maior confiabilidade, especialmente em sistemas de tempo real.
Abaixo, listamos os principais padrões relacionados ao desenvolvimento de controladores de loop fechado:
7.1 Strategy Pattern (Padrão Estratégia)
Esse é um dos mais diretamente aplicáveis ao controle. O Strategy Pattern permite que diferentes algoritmos de controle (PID, Bang-Bang, LQR, etc.) sejam intercambiáveis em tempo de execução, desde que implementem uma interface comum.
Aplicação: Você define uma interface ControlAlgorithm com a função compute(float error). Cada algoritmo implementa essa função de forma diferente.
Vantagens:
- Facilita a troca dinâmica do controlador;
- Permite testes A/B de algoritmos com a mesma infraestrutura de hardware;
- Reutilização de código.
Exemplo em C:
typedef float (*control_function_t)(float error);
typedef struct {
control_function_t compute;
} ControlStrategy;
ControlStrategy pid_controller = { .compute = pid_compute };
ControlStrategy bangbang_controller = { .compute = bangbang_compute };
// No loop de controle:
float u = controller.compute(error);
7.2 State Pattern (Padrão de Estado)
Útil em sistemas com diferentes modos operacionais, como controle ativo, standby, segurança, etc. Cada estado pode usar um algoritmo de controle diferente, ou configurar parâmetros do PID de forma distinta.
Aplicação: Você modela o sistema como uma máquina de estados, e cada estado contém um algoritmo ou conjunto de parâmetros.
Exemplo:
- Estado “Aquecendo” usa PID.
- Estado “Manutenção” usa Bang-Bang.
- Estado “Falha” desliga a saída.
7.3 Singleton Pattern
Em muitos sistemas embarcados, o controlador é um único recurso global. O padrão Singleton garante que apenas uma instância do controlador esteja ativa e acessível globalmente (com cuidado em sistemas com multitarefa).
7.4 Observer Pattern
Ideal para desacoplar o controlador dos sensores e atuadores. O controlador pode ser notificado quando um novo valor de sensor é lido (por exemplo, em RTOS ou eventos baseados em filas).
7.5 Command Pattern
Útil quando se deseja encapsular comandos de controle, por exemplo para registrar comandos enviados, desfazer ações (undo), ou aplicar sequências de controle programadas.
7.6 Aplicação Combinada com RTOS
Em sistemas com sistemas operacionais de tempo real (como FreeRTOS, Zephyr ou ThreadX), o controlador pode ser implementado como uma tarefa que bloqueia esperando um semáforo ou notificação de timer. Os padrões citados ajudam a estruturar essa tarefa:
- O Strategy define a lógica de controle;
- O Observer permite que a tarefa reaja a eventos;
- O State define modos de operação com diferentes estratégias.
Exemplo Integrado:
// Estrutura do controlador com Strategy
typedef struct {
control_function_t compute;
float Kp, Ki, Kd;
} PIDController;
float pid_compute(PIDController* pid, float error) {
// implementação PID com base nos parâmetros
}
Benefícios de usar padrões de projeto no controle:
- Clareza: separa claramente responsabilidades (cálculo, interface, hardware);
- Escalabilidade: facilita a evolução do sistema com novos algoritmos ou estados;
- Testabilidade: permite testes unitários isolados para cada componente;
- Reutilização: mesmo controlador pode ser usado em vários projetos.
8. Modelo de Amostragem: Exemplo Completo de Implementação PID em C
A seguir está um modelo funcional e modularizado de controlador PID em C. Ele pode ser adaptado facilmente para microcontroladores como STM32, AVR, ESP32 ou outros, e segue as boas práticas discutidas nas seções anteriores, incluindo encapsulamento, separação de responsabilidades e proteção contra saturações.
8.1 Arquivo de Cabeçalho – pid.h
#ifndef PID_H
#define PID_H
typedef struct {
float Kp;
float Ki;
float Kd;
float Ts; // Tempo de amostragem em segundos
float integral;
float prev_error;
float output_min;
float output_max;
} PIDController;
// Inicializa os parâmetros do PID
void pid_init(PIDController* pid, float Kp, float Ki, float Kd, float Ts, float min, float max);
// Executa o cálculo do PID
float pid_compute(PIDController* pid, float setpoint, float measurement);
#endif
8.2 Arquivo de Implementação – pid.c
#include "pid.h"
void pid_init(PIDController* pid, float Kp, float Ki, float Kd, float Ts, float min, float max) {
pid->Kp = Kp;
pid->Ki = Ki;
pid->Kd = Kd;
pid->Ts = Ts;
pid->integral = 0.0f;
pid->prev_error = 0.0f;
pid->output_min = min;
pid->output_max = max;
}
float pid_compute(PIDController* pid, float setpoint, float measurement) {
float error = setpoint - measurement;
pid->integral += error * pid->Ts;
// Anti-windup
if (pid->integral > pid->output_max) pid->integral = pid->output_max;
if (pid->integral < pid->output_min) pid->integral = pid->output_min;
float derivative = (error - pid->prev_error) / pid->Ts;
pid->prev_error = error;
float output = pid->Kp * error + pid->Ki * pid->integral + pid->Kd * derivative;
// Saturação da saída
if (output > pid->output_max) output = pid->output_max;
if (output < pid->output_min) output = pid->output_min;
return output;
}
8.3 Exemplo de Uso – main.c
#include <stdio.h>
#include "pid.h"
// Simulação de sensor e atuador
float read_sensor() {
static float y = 0.0f;
return y;
}
void write_actuator(float control_signal) {
printf("Controle aplicado: %.2f\n", control_signal);
}
int main() {
PIDController pid;
pid_init(&pid, 2.0f, 1.0f, 0.5f, 0.01f, 0.0f, 100.0f); // Kp, Ki, Kd, Ts, min, max
float setpoint = 50.0f; // Valor desejado
float process_value = 0.0f;
for (int i = 0; i < 100; i++) {
process_value = read_sensor(); // Aqui pode ser ADC
float u = pid_compute(&pid, setpoint, process_value);
write_actuator(u); // Aqui pode ser PWM
// Simula atualização da variável controlada (pode incluir dinâmica)
}
return 0;
}
8.4 Como Adaptar
- Em tempo real: coloque
pid_compute()em uma ISR de timer (ex: a cada 10 ms). - Leitura real: substitua
read_sensor()por leitura via ADC (HAL ou bare-metal). - Saída real: use
write_actuator()com PWM, DAC ou GPIO para ativar o atuador. - RTOS: execute o controle em uma tarefa periódica com prioridade adequada.
8.5 Extensões Possíveis
- Adicionar limites de velocidade na saída (
du/dt); - Incorporar filtro na entrada (sensor ruidoso);
- Suporte a estratégias de controle alternativas (via ponteiro de função ou enum);
- Log de dados e interface de monitoramento serial.
Conclusão do Modelo
Este exemplo serve como base robusta para qualquer aplicação embarcada com controle de malha fechada. Com pequenas alterações, pode ser usado para sistemas de corrente, temperatura, velocidade, posição, entre outros — tanto em aplicações industriais quanto acadêmicas ou hobby.
Se você conhece ou desenvolveu um algoritmo de controle de loop fechado alternativo — seja uma variação do PID, um controlador adaptativo ou mesmo uma abordagem inovadora baseada em inteligência artificial — convidamos você a colaborar com este conteúdo! Compartilhe sua ideia e o código explicando sua lógica por meio de um GitHub Gist, e envie o link nos comentários ou entre em contato. Sua contribuição poderá enriquecer ainda mais este guia e ajudar outros desenvolvedores e engenheiros na criação de sistemas de controle mais eficientes e criativos.