2 — Fundamentos matemáticos do algoritmo de Goertzel (do zero, passo a passo)
2.1 Onde o Goertzel se encaixa no DSP clássico
No DSP tradicional, quando queremos saber “quais frequências existem” em um sinal, usamos a Transformada Discreta de Fourier (DFT) ou sua versão rápida, a FFT. O problema é que a DFT calcula todos os bins espectrais, mesmo quando estamos interessados em apenas uma ou poucas frequências.
O algoritmo de Goertzel resolve exatamente esse desperdício computacional. Ele calcula um único coeficiente da DFT por vez, usando uma equação recursiva de segunda ordem. Em termos práticos:
- FFT → custo ≈ \(O(N \log N)\)
- Goertzel → custo ≈ \(O(N)\) por frequência de interesse
Se você quer analisar apenas 3 ou 4 frequências (fundamental + harmônicos), o Goertzel é dramaticamente mais eficiente em MCU.
2.2 A DFT vista como um único bin
A DFT de um sinal discreto \(x[n]\) é definida como:
\[
X[k] = \sum_{n=0}^{N-1} x[n];e^{-j2\pi kn/N}
\]
Cada valor de (k) corresponde a uma frequência específica:
\[
f_k = \frac{k}{N} f_s
\]
O algoritmo de Goertzel calcula exatamente um único (X[k]), sem calcular os outros.
2.3 A ideia-chave: um oscilador ressonante discreto
A sacada matemática do Goertzel é reescrever a DFT como um filtro recursivo ressonante, sintonizado na frequência desejada.
Definimos:
\[
\omega_k = \frac{2\pi k}{N}
\]
E o coeficiente:
\[
c = 2\cos(\omega_k)
\]
O algoritmo usa a seguinte recorrência:
\[
s[n] = x[n] + c,s[n-1] – s[n-2]
\]
com condições iniciais:
\[
s[-1] = 0,\quad s[-2] = 0
\]
Essa equação descreve um oscilador digital que:
- Acumula energia se (x[n]) contém a frequência (f_k)
- Cancela energia se o sinal não contém essa frequência
2.4 Extraindo a energia da frequência
Após processar (N) amostras, a energia da frequência (k) é obtida por:
\[
|X[k]|^2 = s[N-1]^2 + s[N-2]^2 – c,s[N-1],s[N-2]
\]
Este valor:
- É proporcional à energia do sinal naquela frequência
- Não depende da fase
- É ideal para detecção (comparação com limiar)
Esse detalhe é crítico para uso em sistemas embarcados:
Não precisamos calcular seno, cosseno ou números complexos em tempo real.
2.5 Relação com filtros IIR de segunda ordem
Observe a recorrência:
\[
s[n] = x[n] + c,s[n-1] – s[n-2]
\]
Ela é estruturalmente idêntica a um filtro IIR de 2ª ordem (biquad), com polos exatamente sobre o círculo unitário na frequência de interesse.
Isso significa que o Goertzel é, conceitualmente:
- Um filtro passa-faixa extremamente estreito
- Com ganho máximo na frequência alvo
- Executado apenas por (N) amostras
Essa interpretação ajuda muito a entender:
- Por que o algoritmo “explode” quando a frequência bate
- Por que ele é sensível a desvios de frequência
- Por que a escolha de (N) é fundamental
2.6 Escolha de (N) e resolução em frequência
A resolução espectral é:
\[
\Delta f = \frac{f_s}{N}
\]
Exemplo com o mesmo cenário do artigo anterior:
- \(f_s = 8000\ \text{Hz}\)
- \(N = 256\)
\[
\Delta f = \frac{8000}{256} \approx 31{,}25\ \text{Hz}
\]
Isso é mais do que suficiente para assobio humano, que:
- Não exige resolução musical fina
- Tem variações naturais bem maiores que 30 Hz
2.7 Como mapeamos frequência real → índice (k)
Dada uma frequência de interesse (f_0):
\[
k = \text{round}\left(\frac{f_0}{f_s} \cdot N\right)
\]
Exemplo:
- \(f_0 = 1500\ \text{Hz}\)
- \(f_s = 8000\ \text{Hz}\)
- \(N = 256\)
\[
k \approx \frac{1500}{8000} \cdot 256 \approx 48
\]
Esse (k) será usado para calcular:
- \(\omega_k\)
- \(c = 2\cos(\omega_k)\)
2.8 O que vamos detectar no assobio
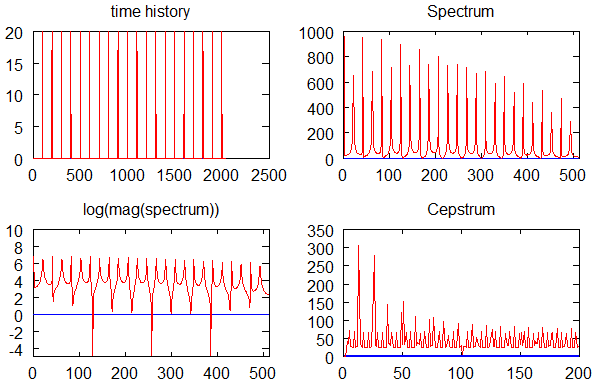
Diferente do cepstrum (que detecta periodicidade), aqui vamos detectar:
- Energia forte em uma frequência fundamental
- Energia coerente em 1º e 2º harmônicos
A estratégia será:
- Executar Goertzel para \(f_0\)
- Executar Goertzel para \(2f_0\)
- Opcionalmente para \(3f_0\)
- Criar um critério espectral composto
Isso reduz drasticamente falsos positivos.