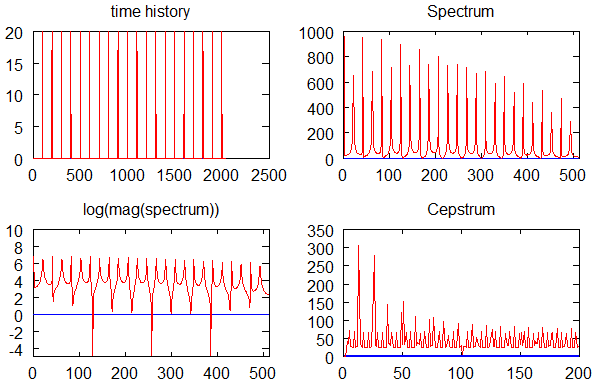
5 — Decisor completo + LED + otimizações (coeficientes pré-computados, EMA, histerese) e integração no RP2040
Nesta seção vamos transformar o “processador de frame” da Seção 4 em um detector de assobio pronto para uso, com:
- Coeficientes do Goertzel pré-computados (evita
cosf()repetido) - Gate por energia
- Critério espectral (fundamental + harmônicos)
- Histerese para evitar “pisca-pisca”
- Suavização temporal (EMA) do score
- Acionamento do LED via GPIO
- Integração com ADC + timer no RP2040
Ainda não é o “arquivo final completo”. Vamos fechar agora a arquitetura; na próxima seção eu entrego o código completo e funcional em um único
main.c, como no artigo anterior.
5.1 Otimização essencial: pré-computar os detectores da varredura
Na Seção 4, goertzel_power_at() calculava k, w, cosf() toda vez. Isso é ótimo para didática, mas em firmware real podemos fazer melhor:
- Criar uma lista de frequências de varredura
- Pré-calcular o coeficiente
coeff = 2*cos(w) - No frame, só rodar a recorrência
5.1.1 Estrutura do “detector preparado”
typedef struct {
float f; // frequência (Hz)
float coeff; // 2*cos(2*pi*k/N)
} goertzel_bin_t;
5.1.2 Construindo a lista de bins (800–3000 Hz, passo 2 bins)
#define FS_HZ 8000
#define FRAME_N 256
#define F_MIN 800.0f
#define F_MAX 3000.0f
#define MAX_BINS 64
static goertzel_bin_t g_bins[MAX_BINS];
static int g_bins_count = 0;
static void goertzel_bins_init(void)
{
const float fs = (float)FS_HZ;
const float df = fs / (float)FRAME_N; // ~31.25 Hz
const float step = 2.0f * df; // ~62.5 Hz
g_bins_count = 0;
for (float f = F_MIN; f <= F_MAX && g_bins_count < MAX_BINS; f += step) {
int k = (int)(0.5f + ((float)FRAME_N * f) / fs);
float w = (2.0f * (float)M_PI * (float)k) / (float)FRAME_N;
g_bins[g_bins_count].f = f;
g_bins[g_bins_count].coeff = 2.0f * cosf(w);
g_bins_count++;
}
}
Agora a varredura não precisa mais de cosf() em runtime.
5.2 Goertzel “rápido” usando coeff pré-calculado
Com coeff pronto, o loop fica bem enxuto:
static float goertzel_power_coeff(const float *x, float coeff)
{
float s1 = 0.0f;
float s2 = 0.0f;
for (int n = 0; n < FRAME_N; n++) {
float s0 = x[n] + coeff * s1 - s2;
s2 = s1;
s1 = s0;
}
return (s1*s1) + (s2*s2) - (coeff*s1*s2);
}
5.3 Encontrar o melhor candidato f0 (varredura)
static float find_best_f0_fast(const float *frame, float *p0_out)
{
float best_f = g_bins[0].f;
float best_p = -1.0f;
for (int i = 0; i < g_bins_count; i++) {
float p = goertzel_power_coeff(frame, g_bins[i].coeff);
if (p > best_p) {
best_p = p;
best_f = g_bins[i].f;
}
}
if (p0_out) *p0_out = best_p;
return best_f;
}
5.4 Harmônicos com cálculo “on demand”
Para harmônicos, não vale manter tabela grande. A gente calcula coeff pontualmente:
static inline float coeff_for_freq(float f)
{
const float fs = (float)FS_HZ;
int k = (int)(0.5f + ((float)FRAME_N * f) / fs);
float w = (2.0f * (float)M_PI * (float)k) / (float)FRAME_N;
return 2.0f * cosf(w);
}
static float power_at_freq(const float *frame, float f)
{
float c = coeff_for_freq(f);
return goertzel_power_coeff(frame, c);
}
5.5 Critério espectral composto (score)
Agora vamos criar um score numérico em vez de true/false. Isso facilita EMA e histerese.
Uma forma boa e simples:
p0: potência no candidato f0p2: potência em 2f0p3: potência em 3f0 (se existir)- Normalização por energia do frame (para não depender do volume)
Score proposto:
\[
S = \frac{p0}{E+\epsilon} + \lambda_2\frac{p2}{p0+\epsilon} + \lambda_3\frac{p3}{p0+\epsilon}
\]
Implementação:
static float frame_energy(const float *x)
{
float acc = 0.0f;
for (int i = 0; i < FRAME_N; i++) acc += x[i] * x[i];
return acc / (float)FRAME_N;
}
static float compute_whistle_score(const float *frame, float *f0_out)
{
const float eps = 1e-9f;
float E = frame_energy(frame);
if (E < E_MIN) return 0.0f;
float p0 = 0.0f;
float f0 = find_best_f0_fast(frame, &p0);
float f2 = 2.0f * f0;
float f3 = 3.0f * f0;
const float nyq = 0.5f * (float)FS_HZ;
float p2 = (f2 <= nyq) ? power_at_freq(frame, f2) : 0.0f;
float p3 = (f3 <= nyq) ? power_at_freq(frame, f3) : 0.0f;
// pesos práticos
const float l2 = 0.7f;
const float l3 = 0.35f;
float s0 = p0 / (E + eps);
float r2 = p2 / (p0 + eps);
float r3 = p3 / (p0 + eps);
float S = s0 + l2 * r2 + l3 * r3;
if (f0_out) *f0_out = f0;
return S;
}
5.6 Decisão robusta com EMA + histerese
S_filt = EMA(S)- Liga quando
S_filt > S_ON - Desliga quando
S_filt < S_OFF
static float g_S_filt = 0.0f;
static bool g_state = false;
static void update_led_from_score(float S, float f0, uint led_gpio)
{
// suaviza
g_S_filt = EMA_ALPHA * g_S_filt + (1.0f - EMA_ALPHA) * S;
// sanity: garante faixa típica do assobio
bool f_ok = (f0 >= 700.0f && f0 <= 3500.0f);
// limiares iniciais (calibração depois)
const float S_ON = 25.0f;
const float S_OFF = 18.0f;
if (!g_state) {
if (f_ok && g_S_filt > S_ON) g_state = true;
} else {
if (!f_ok || g_S_filt < S_OFF) g_state = false;
}
gpio_put(led_gpio, g_state ? 1 : 0);
}
Esses valores (
S_ON,S_OFF) dependem do microfone, do ganho e do ambiente — mas o formato do score torna a calibração bem mais previsível do que limiar bruto emp0.
5.7 Integração de tempo real (ADC + DC-block + frame)
Vamos unir tudo num fluxo igual ao artigo anterior.
5.7.1 DC-block
typedef struct {
float mean;
} dc_block_t;
static inline void dc_block_init(dc_block_t *d) { d->mean = 0.0f; }
static inline float dc_block_step(dc_block_t *d, float x)
{
const float beta = 0.0015f;
d->mean += beta * (x - d->mean);
return x - d->mean;
}
5.7.2 Estado global e callback de amostragem
static frame_buf_t g_frame;
static dc_block_t g_dc;
static bool sample_timer_cb(repeating_timer_t *rt)
{
(void)rt;
float x = read_adc_normalized();
x = dc_block_step(&g_dc, x);
frame_buf_push(&g_frame, x);
return true;
}
5.7.3 Loop processa frame e atualiza LED
static void process_frame_if_ready(uint led_gpio)
{
if (!g_frame.full) return;
g_frame.full = false;
float f0 = 0.0f;
float S = compute_whistle_score(g_frame.data, &f0);
update_led_from_score(S, f0, led_gpio);
}