LPCC (Linear Prediction Cepstral Coefficients): Fundamentos, Algoritmos e Aplicações em Sistemas Embarcados

2 — LPCC (Linear Prediction Cepstral Coefficients)

O que significa LPCC

LPCC é o acrônimo de Linear Prediction Cepstral Coefficients (Coeficientes Cepstrais por Predição Linear).

Enquanto o LPC descreve o sinal como um modelo de filtro tudo-polo, o LPCC descreve esse mesmo modelo no domínio cepstral, o que traz vantagens fundamentais para análise, comparação e aprendizado de máquina.

Em termos conceituais:

• LPC → modela como o sinal é gerado
• LPCC → descreve as características espectrais do modelo

Essa mudança de domínio é crucial porque o domínio cepstral desacopla parcialmente fonte e filtro, tornando os coeficientes mais robustos para classificação e reconhecimento de padrões.

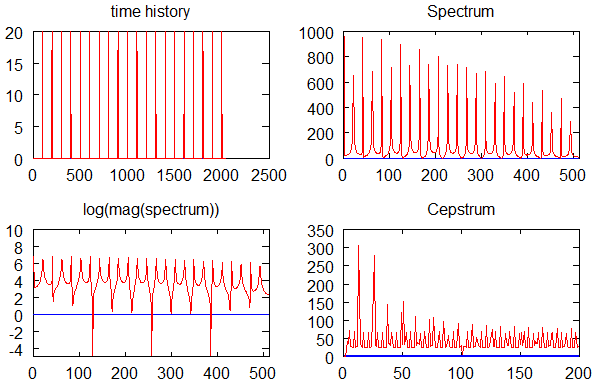
O que é o domínio cepstral (intuição)

O termo cepstrum vem de uma inversão proposital de letras (spectrum → cepstrum).

A ideia central é:

1. O espectro de um sinal é multiplicativo
2. O logaritmo transforma multiplicação em soma
3. A transformada inversa (IDFT ou série equivalente) separa componentes lentas e rápidas

No caso do LPCC:

• Não se usa FFT diretamente
• O cepstrum é derivado analiticamente a partir dos coeficientes LPC
• Isso reduz custo computacional e mantém coerência com o modelo tudo-polo

Relação matemática entre LPC e LPCC

Dado um modelo LPC de ordem ( p ), com coeficientes ( a_k ), os coeficientes cepstrais ( c_n ) são calculados recursivamente:

\[
c_0 = \ln(\sigma^2)
\]

\[
c_n = a_n + \sum_{k=1}^{n-1} \frac{k}{n} , c_k , a_{n-k}
\quad \text{para } 1 \le n \le p
\]

\[
c_n = \sum_{k=n-p}^{n-1} \frac{k}{n} , c_k , a_{n-k}
\quad \text{para } n > p
\]

onde:

• \( a_k \) → coeficientes LPC
• \( c_n \) → coeficientes cepstrais
• \( \sigma^2 \) → variância do erro de predição

Esse ponto é crítico:

LPCC não exige FFT, DCT ou IFFT
Tudo é feito por recorrência algébrica, ideal para firmware.

Por que LPCC é preferível ao LPC em Machine Learning

Do ponto de vista prático:

• LPC é sensível a:
  • Ruído
  • Quantização
  • Pequenas variações espectrais
• LPCC:
  • Tem melhor separabilidade de classes
  • É mais estável numericamente
  • Possui interpretação geométrica no espaço de características

Por isso:

• Reconhecimento de fala clássico
• Classificação acústica
• Análise vibroacústica
• Detecção de padrões mecânicos

costumam preferir LPCC em vez de LPC puro.

Implementação em C — LPC → LPCC

Abaixo um exemplo direto, fiel ao artigo de referência, mas em C, pensado para sistemas embarcados.

#include <math.h>
#include <stddef.h>

/**
 * Converte coeficientes LPC em coeficientes LPCC
 * lpc     : coeficientes LPC (a[1..p])
 * p       : ordem LPC
 * cep     : coeficientes cepstrais (c[0..n_cep-1])
 * n_cep   : número de coeficientes cepstrais desejados
 * error   : variância do erro de predição
 */
void lpc_to_lpcc(const float *lpc,
                 size_t p,
                 float *cep,
                 size_t n_cep,
                 float error)
{
    cep[0] = logf(error);

    for (size_t n = 1; n < n_cep; n++) {
        float sum = 0.0f;

        size_t k_max = (n < p) ? n : p;

        for (size_t k = 1; k < k_max; k++) {
            sum += ((float)k / (float)n) * cep[k] * lpc[n - k - 1];
        }

        if (n <= p) {
            cep[n] = lpc[n - 1] + sum;
        } else {
            cep[n] = sum;
        }
    }
}

#include <math.h>
#include <stddef.h>

/**
 * Converte coeficientes LPC em coeficientes LPCC
 * lpc     : coeficientes LPC (a[1..p])
 * p       : ordem LPC
 * cep     : coeficientes cepstrais (c[0..n_cep-1])
 * n_cep   : número de coeficientes cepstrais desejados
 * error   : variância do erro de predição
 */
void lpc_to_lpcc(const float *lpc,
                 size_t p,
                 float *cep,
                 size_t n_cep,
                 float error)
{
    cep[0] = logf(error);

    for (size_t n = 1; n < n_cep; n++) {
        float sum = 0.0f;

        size_t k_max = (n < p) ? n : p;

        for (size_t k = 1; k < k_max; k++) {
            sum += ((float)k / (float)n) * cep[k] * lpc[n - k - 1];
        }

        if (n <= p) {
            cep[n] = lpc[n - 1] + sum;
        } else {
            cep[n] = sum;
        }
    }
}

Observações importantes sobre o código

Alguns pontos que merecem atenção técnica:

• Índices em C começam em zero, mas as fórmulas assumem índices matemáticos
• lpc[n - 1] corresponde a ( a_n )
• cep[0] carrega informação de energia (log do erro)
• É comum:
  • Descartar c0
  • Usar apenas c1 até c12 ou c16

Essas decisões dependem da aplicação.

Complexidade computacional

Para firmware e IoT:

• Complexidade: ( O(N \cdot p) )
• Não usa FFT
• Pode rodar:
  • Em Cortex-M
  • Em RISC-V
  • Em DSPs simples

Isso torna LPCC muito atraente para edge AI clássico, sem redes neurais.