LPCC (Linear Prediction Cepstral Coefficients): Fundamentos, Algoritmos e Aplicações em Sistemas Embarcados

5 — AC (Autocorrelation)

O que significa AC

AC é o acrônimo de Autocorrelation (Autocorrelação).
No contexto de LP, LPC e LPCC, a autocorrelação não é um detalhe matemático, mas sim o mecanismo central que permite estimar os coeficientes de predição de forma estável e eficiente.

Em termos simples:

A autocorrelação mede o quanto um sinal se parece consigo mesmo quando deslocado no tempo.

Ela captura estrutura, periodicidade e dependência temporal, exatamente o que a predição linear explora.

Definição matemática da autocorrelação

Para um sinal discreto ( x[n] ), a autocorrelação é definida como:

\[
r[k] = \sum_{n=k}^{N-1} x[n] \cdot x[n-k]
\]

onde:

• \( k \) é o atraso (lag)
• \( N \) é o tamanho da janela de análise

Esse conjunto de valores \( r[0], r[1], \dots, r[p] \) forma o vetor de autocorrelação, usado diretamente nas equações LPC.

Por que a autocorrelação é usada em LPC

Existem três razões fundamentais para o uso da autocorrelação:

1. Garante estabilidade do filtro LPC

O método da autocorrelação leva a uma matriz de Toeplitz simétrica e positiva definida, o que assegura:

• Polos dentro do círculo unitário
• Filtro estável
• Levinson-Durbin aplicável

2. Reduz sensibilidade a ruído

A soma ao longo do tempo atua como um suavizador estatístico, reduzindo flutuações locais.

3. Conecta LP a mínimos quadrados

A minimização do erro médio quadrático da predição resulta naturalmente nas equações normais, expressas em termos de autocorrelação.

Equações de Yule-Walker

A partir da autocorrelação, o problema de LP resulta nas equações de Yule-Walker:

\[
\sum_{k=1}^{p} a_k , r[|i-k|] = -r[i]
\quad \text{para } i = 1, 2, \dots, p
\]

Essas equações relacionam:

• Autocorrelação do sinal
• Coeficientes LPC
• Erro mínimo de predição

Resolver esse sistema de forma eficiente é exatamente o papel do algoritmo de Levinson-Durbin (próxima seção).

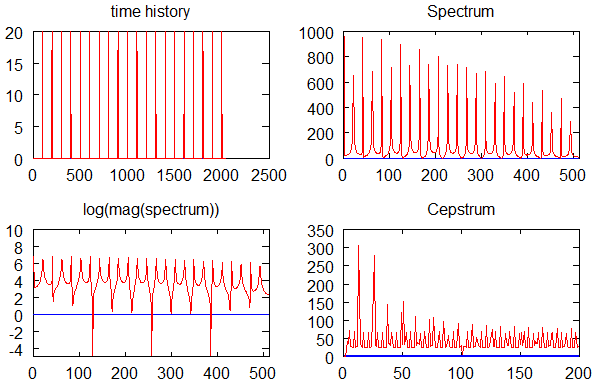
Interpretação física da autocorrelação

A autocorrelação responde perguntas como:

• O sinal tem periodicidade?
• Existe memória temporal?
• O comportamento passado influencia o presente?

Exemplos:

• Fala → picos relacionados ao pitch
• Vibração mecânica → ressonâncias estruturais
• Ruído branco → autocorrelação quase nula fora de \( k = 0 \)

Isso explica por que LPC funciona mal para ruído branco e bem para sinais estruturados.

Autocorrelação e estacionariedade

Um ponto conceitual importante:

O método LPC assume estacionariedade local do sinal.

Ou seja:

• As estatísticas não mudam significativamente dentro da janela analisada
• A autocorrelação é válida apenas nesse intervalo

Por isso, na prática:

• O sinal é dividido em janelas curtas
• Cada janela gera um conjunto LPC/LPCC próprio

Implementação em C — autocorrelação (revisão prática)

Aqui está um exemplo claro e reutilizável em C, adequado para firmware:

/**
 * Calcula a autocorrelação de um sinal
 */
void autocorrelation(const float *x,
                     size_t N,
                     size_t p,
                     float *r)
{
    for (size_t k = 0; k <= p; k++) {
        float sum = 0.0f;

        for (size_t n = k; n < N; n++) {
            sum += x[n] * x[n - k];
        }

        r[k] = sum;
    }
}

/**
 * Calcula a autocorrelação de um sinal
 */
void autocorrelation(const float *x,
                     size_t N,
                     size_t p,
                     float *r)
{
    for (size_t k = 0; k <= p; k++) {
        float sum = 0.0f;

        for (size_t n = k; n < N; n++) {
            sum += x[n] * x[n - k];
        }

        r[k] = sum;
    }
}

Esse vetor r[] é entrada direta para Levinson-Durbin.

Consequências práticas em sistemas embarcados

• Custo computacional: ( O(N \cdot p) )
• Pode ser otimizado com:
  • Buffers circulares
  • DMA
  • Janela fixa
• Funciona bem em:
  • Cortex-M
  • RISC-V
  • DSPs simples

A autocorrelação é barata e confiável — por isso é tão usada.