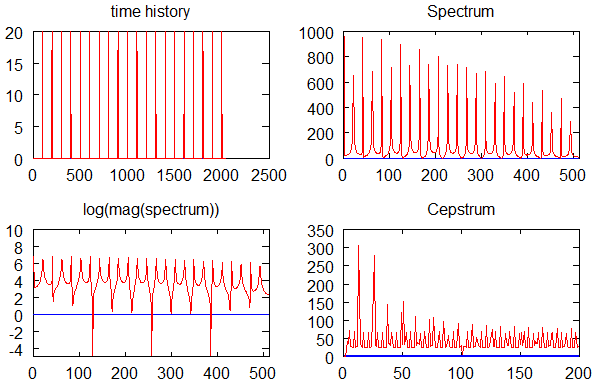
Introdução: por que falar em Quefrequência e Análise Cepstral?
Quando trabalhamos com áudio em sistemas embarcados (como um ESP32-P4), é muito comum pensar apenas em tempo e frequência: sinal no tempo, depois FFT para ver o espectro, aplicar filtros, etc. Porém, há situações em que olhar somente o espectro de magnitude não é suficiente para separar os “componentes” de interesse do sinal:
- Separar o conteúdo de excitação (por exemplo, cordas vocais ou fonte sonora) do “formante” ou ressonâncias do sistema (trato vocal, sala, caixa acústica).
- Identificar ecos ou reverberações (reflexões) embutidos no sinal.
- Estimar pitch (frequência fundamental da voz) mesmo em ambientes ruidosos ou com filtragem forte.
- Detectar características de envoltória espectral (timbre) independentemente da excitação instantânea.
A análise cepstral foi criada justamente para isso: ela “desfaz” a convolução no domínio da frequência ao transformar multiplicações em somas usando o logaritmo, e depois aplica novamente uma transformada inversa. Isso gera um novo domínio de análise – não mais tempo, nem frequência – mas o domínio da quefrequência.
Conceito intuitivo de Quefrequência
O termo “quefrequência” é um trocadilho proposital com “frequency” (frequência). A ideia é:
- No domínio da frequência, o eixo horizontal é a frequência ( f ) (Hz).
- Na análise cepstral, depois de aplicar log do espectro e uma transformada inversa, o eixo horizontal passa a ter unidade de tempo, mas não é o tempo original do sinal; é um “tempo de periodicidade” derivado da estrutura de frequência.
- Como essa variável não é exatamente o tempo do domínio original, nem a frequência, foi dado o nome de quefrequência e a unidade de queferência (em segundos ou amostras, mas interpretada como “período da estrutura espectral”).
Intuitivamente:
- Picos de periodicidade de pitch aparecem como picos em quefrequência correspondendo ao período fundamental do sinal.
- A envoltória lenta do espectro (por exemplo, os formantes da voz ou a resposta de uma sala) aparece concentrada em baixas quefrequências.
- Componentes mais “rápidos” do espectro (finas linhas espectrais, harmônicos) aparecem em quefrequências mais altas.
Isso permite “separar no eixo da quefrequência” aquilo que queremos analisar:
- Baixa quefrequência → envoltória espectral (formantes, timbre, resposta de sistema).
- Alta quefrequência → detalhes finos da excitação (harmônicos, rugosidade, etc.).
Em processamento de voz, isso tem aplicações clássicas:
- Modelagem fonte–filtro: a fala é modelada como excitação (cordas vocais ou ruído glótico) passando por um filtro (trato vocal). A análise cepstral permite separar esses dois componentes.
- Reconhecimento de fala: coeficientes cepstrais (por exemplo, MFCC – Mel Frequency Cepstral Coefficients) são onipresentes em sistemas de ASR.
- Equalização e cancelamento de eco: a estrutura de eco pode ser observada no domínio cepstral e tratada de forma mais clara em alguns cenários.
No contexto do ESP32-P4 e de sistemas embarcados em geral, a análise cepstral é interessante porque:
- Pode ser implementada em cima de FFTs já disponíveis (bibliotecas de DSP, ESP-DSP, etc.).
- É computacionalmente viável para janelas de áudio de tamanho moderado.
- Fornece uma representação compacta do sinal (poucos coeficientes cepstrais podem ser suficientes para muitos algoritmos de decisão, classificação ou detecção).
Visão global do fluxo de análise cepstral
Sem entrar ainda nos detalhes matemáticos (que virão na próxima seção), o fluxo básico é:
- Janelação do sinal no tempo
Pegamos um bloco de amostras \( x[n] \) (por exemplo, 256, 512 ou 1024 amostras) e aplicamos uma janela \( w[n] \) (Hann, Hamming, etc.) para reduzir descontinuidades. - Transformada de Fourier (FFT)
Calculamos o espectro complexo:
\[
X[k] = \text{FFT}{ x[n] \cdot w[n] }
\]
Obtemos magnitude (|X[k]|) e fase \(\angle X[k]\). - Logaritmo da magnitude
Calculamos o logaritmo \(natural ou base 10\) da magnitude:
\[
Y[k] = \log(|X[k]|)
\]
Isso transforma produtos (decorrentes da convolução no tempo) em somas no domínio espectral. - Transformada de Fourier inversa (IFFT)
Fazemos a IFFT de ( Y[k] ):
\[
c[n] = \text{IFFT}{ Y[k] }
\]
O sinal \( c[n] \) é o cepstro do quadro de áudio, e o índice ( n ) agora é interpretado como quefrequência. - Análise dos coeficientes cepstrais
- Coeficientes próximos de ( n = 0 ) (baixa quefrequência) descrevem a envoltória lenta do espectro.
- Coeficientes em quefrequências maiores podem indicar periodicidade (pitch) e detalhes finos.
Na prática, em um ESP32-P4, esse fluxo pode ser implementado em tempo quase real, usando:
- DMA + I2S para adquirir áudio.
- FFT otimizada em ponto fixo ou flutuante (conforme os recursos).
- Um pipeline de janelas de áudio para extrair cepstro quadro a quadro (por exemplo, a cada 10–20 ms).
Nas próximas seções, vamos:
- Escrever as fórmulas matemáticas formais da análise cepstral (domínio contínuo e discreto, convolução, FFT, log-espectro, IFFT, quefrequência).
- Discutir a interpretação física e prática do cepstro e da quefrequência, com exemplos típicos em áudio.
- Apresentar códigos em C para ESP32-P4, com:
- Aquisição de áudio (mock ou usando I2S).
- Cálculo da FFT, log-espectro e IFFT para obter o cepstro.
- Extração de coeficientes de baixa quefrequência para uso em algoritmos de decisão (por exemplo, detecção de voz, pitch simplificado, ou caracterização de timbre).
2 – Fundamentos Matemáticos da Análise Cepstral e da Quefrequência
A análise cepstral nasce da necessidade de separar efeitos de convolução entre um sinal de excitação e a resposta de um sistema. Em áudio, isso aparece no modelo clássico fonte–filtro, mas o conceito é geral: sempre que um sinal ( x(t) ) resulta da convolução entre dois sinais ( s(t) ) e ( h(t) ), o cepstro ajuda a separar essas contribuições.
2.1 O ponto de partida: convolução no tempo → multiplicação na frequência
Seja um sinal:
\[
x(t) = s(t) * h(t)
\]
onde:
- \( s(t) \): excitação (por exemplo, vibrato das cordas vocais).
- \( h(t) \): filtro (por exemplo, trato vocal ou resposta de uma sala).
Pela transformada de Fourier:
\[
X(\omega) = S(\omega) \cdot H(\omega)
\]
A multiplicação complica a interpretação do espectro quando queremos isolar \( S(\omega) \) e \( H(\omega) \).
A solução clássica é aplicar logaritmo:
\[
\log |X(\omega)| = \log |S(\omega)| + \log |H(\omega)|
\]
Isto é fundamental: o log converte produtos em somas, tornando possível uma “separação” térmica entre efeitos rápidos e lentos no domínio espectral.
2.2 Cepstro como IFFT do log-espectro
A definição formal do cepstro real é:
\[
c(t) = \mathcal{F}^{-1}\left{ \log |X(\omega)| \right}
\]
O sinal \( c(t) \) não está mais no domínio do tempo original. O eixo ( t ) passa a ser interpretado como quefrequência, e sua unidade não é frequência, mas sim algo dimensionalmente equivalente ao tempo — porém não o tempo físico.
Por isso, usa-se notação humorística criada pelo grupo de Bogert (inventores do cepstro):
- tempo → quetime
- frequência → quefrequência
- espectro → espectro
- cepstro → cepstrum
- convolução → convolução
- filtro → lifter (filtro no domínio do cepstro)
No domínio discreto, para uma janela ( x[n] ), temos:
\[
X[k] = \text{FFT}{x[n]}
\]
\[
C[n] = \text{IFFT}\left{\log(|X[k]|)\right}
\]
onde:
- \( k = 0, 1, …, N-1 \) é o índice de frequência,
- \( n = 0, 1, …, N-1 \) é o índice de quefrequência.
2.3 Separação entre excitação e envoltória espectral
A interpretação prática decorre da análise de periodicidades:
- A excitação ( s(t) ), quando periódica (como voz sonora), gera um espectro composto por harmônicos espaçados.
Esses harmônicos introduzem padrões rápidos no espectro → aparecem em quefrequências altas. - O filtro ( h(t) ) representa a forma da garganta, microfone, sala, etc., produzindo variações lentas na magnitude espectral (formantes, equalização).
Essas variações lentas → aparecem em quefrequências baixas.
Portanto:
\[
C[n] = C_s[n] + C_h[n]
\]
e como:
- \( C_h[n] \) está concentrado em pequenos valores de ( n ),
- \( C_s[n] \) está concentrado em valores mais altos,
fica simples isolá-los truncando ou filtrando o cepstro.
2.4 Pitch a partir da quefrequência
Se o sinal contém um período dominante \( T_0 \), sua frequência fundamental é:
\[
f_0 = \frac{1}{T_0}
\]
No domínio cepstral, surge um pico aproximadamente em:
\[
n_0 \approx \frac{T_0}{\Delta t}
\]
onde \( \Delta t = \frac{1}{f_s} \) é o período de amostragem.
Por exemplo, em voz humana, com pitch entre 80 e 300 Hz:
- \( T_0 \approx 3,3 \text{ ms a } 12,5 \text{ ms} \)
- Em um sistema com 16 kHz de amostragem: \[
n_0 \approx [53\text{ a }200] \text{ amostras}
\]
Assim, basta procurar o máximo do cepstro em uma faixa adequada.
2.5 Cepstro em sistemas embarcados: por que é eficiente?
A análise cepstral é muito eficiente computacionalmente porque:
- Reutiliza FFT/IFFT já comuns em DSP.
- Usa apenas operações elementares (log, magnitude, FFT inversa).
- Pode ser reduzida a poucos coeficientes (por exemplo, primeiros 12 CEPSTRAIS).
Isso torna o método adequado para o ESP32-P4, que conta com:
- Núcleos de processamento de 32 bits com boa capacidade de DSP.
- Instruções aceleradas para MACs e operações vetoriais.
- Suporte a bibliotecas otimizadas, como ESP-DSP.
3 – Interpretação Prática da Quefrequência em Áudio
A análise cepstral não é apenas uma manobra matemática elegante; ela é extremamente prática quando lidamos com sinais acústicos reais. Nesta seção, vamos interpretar o que significa observar um sinal no domínio da quefrequência e como isso permite separar componentes que, no domínio da frequência tradicional, aparecem misturados.
3.1 Separação Fonte–Filtro: o coração da análise cepstral
Em áudio — especialmente em voz e instrumentos — um modelo universal é:
\[
x(t) = s(t) * h(t)
\]
onde:
- \( s(t) \) é a excitação (cordas vocais, palheta, ruído, golpe mecânico),
- \( h(t) \) é o filtro acústico (trato vocal, corpo do instrumento, caixa acústica, reverberação).
Esse modelo implica:
\[
X(\omega) = S(\omega)\cdot H(\omega)
\]
Quando analisamos o espectro convencional, os efeitos de excitação e filtro aparecem multiplicados. O buraco que a análise cepstral preenche é justamente desmultiplicar esses efeitos — o que não é possível diretamente através da FFT, mas se torna possível usando o log-espectro + IFFT.
O que acontece no cepstro?
Após o processo:
\[
C[n] = \text{IFFT}{\log(|X[k]|)},
\]
a estrutura se reorganiza de forma surpreendente:
- Variações lentas do espectro (formantes, equalização, formato do corpo do instrumento) aparecem próximas de n = 0.
- Variações rápidas, como harmônicos resultantes de excitações periódicas, aparecem em quefrequências maiores.
É como se a análise cepstral “esticava” o espectro em um domínio onde cada tipo de efeito possui uma assinatura clara e separável.
3.2 Estimativa de Pitch (Fundamental) no Cepstro
Uma das aplicações mais conhecidas do cepstro é a detecção de pitch.
Considere um sinal periódico com período fundamental \( T_0 \). Um espectro composto por harmônicos cria uma estrutura repetitiva. O log-espectro evidencia essas repetições e a IFFT devolve um pico em:
\[
n_0 \approx \frac{T_0}{\Delta t},
\quad \Delta t = \frac{1}{f_s}.
\]
Interpretando:
- O pico ocorre aproximadamente na quefrequência que representa o período do sinal.
- Assim, basta localizar o máximo em uma janela adequada para extrair pitch.
Exemplo prático:
Para amostragem a 16 kHz e pitch de 200 Hz:
\[
T_0 = 5 \text{ ms} \quad \Rightarrow \quad n_0 \approx 80.
\]
Logo, buscar picos entre 50 e 250 amostras é suficiente para detectar a maior parte da voz humana.
Essa abordagem funciona bem mesmo quando:
- O espectro está suavizado,
- Há ruído moderado,
- O sinal sofreu filtragens/acústicas conhecidas ou não lineares.
3.3 Detecção de Envoltória Espectral (Timbre)
Os primeiros coeficientes do cepstro representam a envelopa espectral, que define o timbre de instrumentos e da voz.
Em reconhecimento de fala, isso inspira técnicas clássicas como:
- LPC (Linear Predictive Coding),
- MFCC (Mel-Frequency Cepstral Coefficients).
A ideia é simples:
- Os coeficientes de baixa quefrequência capturam a forma geral do espectro.
- Pequenos conjuntos (12 a 20 coeficientes) representam bem o timbre.
Isso se torna extremamente útil em sistemas embarcados para:
- Classificação de sons (porta batendo, voz, motor, música).
- Detecção de eventos acústicos (EDA).
- Reconhecimento de comandos por voz com baixa complexidade.
3.4 Detecção de Eco e Reverberação
Uma propriedade menos conhecida — mas muito poderosa — é a capacidade de observar ecos no domínio cepstral.
Quando um eco ocorre com atraso \( \tau \), a convolução com uma versão atrasada do sinal adiciona um componente periódico no espectro. No cepstro, isso aparece como um pico em:
\[
n_\tau \approx \frac{\tau}{\Delta t}.
\]
Exemplo:
- Um eco com 10 ms de atraso → pico na quefrequência correspondente a 10 ms.
- Uma reverberação mais longa produz uma faixa de quefrequências com energia distribuída.
Isso é útil para:
- Cancelamento de eco,
- Algoritmos de de-reverberação,
- Diagnóstico acústico (testes de salas, tubulações, painéis mecânicos).
3.5 Resumo interpretativo da quefrequência
| Região da Quefrequência | Significado | Fenômenos representados |
|---|---|---|
| Muito baixa (n ≈ 0–10) | Envoltória espectral lenta | Formantes da voz, resposta de caixa, equalização |
| Baixa (n ≈ 10–40) | Estruturas amplas do filtro | Timbre geral do instrumento |
| Média (n ≈ 50–250) | Períodos da excitação | Pitch, harmônicos |
| Alta (n > 250) | Detalhes rápidos e ruído | Textura sonora, fricativas, aspereza |
Este mapeamento orienta como “ler” um cepstro e como projetar algoritmos que exploram o método.
4 – Implementação Prática da Análise Cepstral no ESP32-P4
Nesta seção entramos no nível operacional: como implementar, no ESP32-P4, o pipeline completo da análise cepstral — desde a captura de áudio até a obtenção do vetor de coeficientes no domínio da quefrequência.
O ESP32-P4 possui um núcleo de desempenho superior às gerações anteriores, com instruções otimizadas para DSP, permitindo executar FFT/IFFT e operações vetoriais com boa eficiência mesmo em janelas de 512 ou 1024 amostras. A biblioteca ESP-DSP facilita bastante esse processo, pois contém FFTs altamente otimizadas.
A seguir, apresento o pipeline completo e exemplos de código baseados no ESP-IDF + ESP-DSP.
4.1 Pipeline de processamento do cepstro
O processo no microcontrolador segue:
- Capturar um quadro de áudio via I2S (1024 amostras, por exemplo).
- Aplicar janela Hann ou Hamming.
- Fazer FFT real → espectro complexo.
- Obter magnitude.
- Aplicar logaritmo.
- Fazer IFFT para obter o cepstro.
- Analisar quefrequências de interesse.
Representando matematicamente para ( N ) amostras:
\[
X[k] = \text{FFT}{ x[n] \cdot w[n] }
\]
\[
Y[k] = \log(|X[k]| + \epsilon)
\]
\[
C[n] = \text{IFFT}{ Y[k] }
\]
O termo \( \epsilon \) evita log(0), tipicamente \( \epsilon = 10^{-12} \).
4.2 Estrutura básica do código no ESP32-P4
A seguir um esqueleto funcional em C, com comentários detalhados e adequado ao ESP-IDF.
Inclui:
- Janela Hann
- FFT real
- Cálculo de magnitude + log
- IFFT
- Extração de pitch via busca de máximo na faixa de quefrequência

Código: Inicialização do módulo DSP
/**
* @brief Inicializa a biblioteca ESP-DSP para FFTs
*/
static void init_dsp()
{
// Inicializa tabelas de FFT internas.
dsps_fft2r_init_fc32(NULL, CONFIG_DSP_MAX_FFT_SIZE);
}
4.3 Aplicação da janela Hann
/**
* @brief Aplica janela Hann ao buffer de entrada
*/
static void apply_hann(float *data, int N)
{
for (int n = 0; n < N; n++) {
float w = 0.5f * (1 - cosf((2 * M_PI * n) / (N - 1)));
data[n] *= w;
}
}
4.4 FFT + cálculo da magnitude + log
void compute_log_spectrum(const float *input, float *log_spec, int N)
{
// Buffer complexo para FFT (intercalado real/imag)
static float fft_buf[2048];
// Copia entrada para buffer da FFT
for (int i = 0; i < N; i++) {
fft_buf[2*i] = input[i]; // parte real
fft_buf[2*i+1] = 0.0f; // parte imaginária
}
// FFT real
dsps_fft2r_fc32(fft_buf, N);
dsps_bit_rev_fc32(fft_buf, N);
// Calcula magnitude e log
for (int k = 0; k < N; k++) {
float real = fft_buf[2*k];
float imag = fft_buf[2*k+1];
float mag = sqrtf(real*real + imag*imag);
log_spec[k] = logf(mag + 1e-12f);
}
}
4.5 IFFT para obter o Cepstro
void compute_cepstrum(const float *log_spec, float *cep, int N)
{
static float buf[2048];
// Copia log-espectro para o buffer complexo
for (int k = 0; k < N; k++) {
buf[2*k] = log_spec[k];
buf[2*k+1] = 0.0f;
}
// IFFT
dsps_fft2r_fc32(buf, N);
dsps_bit_rev_fc32(buf, N);
// Saída real do cepstro
for (int n = 0; n < N; n++) {
cep[n] = buf[2*n] / N; // normalização
}
}
4.6 Extração de pitch a partir da quefrequência
O pitch aparece como o pico dominante em uma faixa de quefrequências que representa períodos possíveis da excitação.
Por exemplo, para voz humana em 16 kHz:
- pitch de 80–300 Hz → períodos entre 3,3 ms e 12,5 ms → 53–200 amostras.
/**
* @brief Estima pitch a partir do cepstro
*
* @param cep Vetor de cepstro
* @param fs Taxa de amostragem
* @param N Tamanho do cepstro
*
* @return Frequência fundamental estimada
*/
float estimate_pitch_from_cepstrum(const float *cep, int fs, int N)
{
int min_q = fs / 300; // ~53
int max_q = fs / 80; // ~200
int max_index = min_q;
float max_val = cep[min_q];
for (int n = min_q; n < max_q; n++) {
if (cep[n] > max_val) {
max_val = cep[n];
max_index = n;
}
}
// período estimado
float T0 = (float)max_index / fs;
return 1.0f / T0;
}
4.7 Extração dos primeiros coeficientes cepstrais (para classificação)
Em muita aplicações (classificação acústica, detecção de eventos), apenas os primeiros coeficientes cepstrais são necessários.
/**
* @brief Copia os primeiros M coeficientes do cepstro
*/
void extract_cepstral_coeffs(const float *cep, float *out, int M)
{
for (int i = 0; i < M; i++) {
out[i] = cep[i];
}
}
4.8 Pipeline completo (função principal)
void process_audio_frame(float *frame, int N, int fs)
{
static float log_spec[1024];
static float cep[1024];
apply_hann(frame, N);
compute_log_spectrum(frame, log_spec, N);
compute_cepstrum(log_spec, cep, N);
float pitch = estimate_pitch_from_cepstrum(cep, fs, N);
printf("Pitch estimado: %.2f Hz\n", pitch);
}
4.9 Observações de implementação no ESP32-P4
- Memória
FFT de 1024 pontos requer buffers complexos de 2048 floats → 8 KB.
O ESP32-P4 suporta isso confortavelmente. - Desempenho
Com clock adequado, é possível analisar um quadro de 1024 amostras em menos de 5 ms. - Precisão
Sugere-se usarfloat(32 bits). Em sistemas críticos, é possível migrar para ponto fixo. - Aquisição de áudio real
Basta integrar esta pipeline à captura I2S + DMA, substituindo oframe[]preenchido por dados do ADC/I2S.
5 – Conclusão e Aplicações Práticas em Sistemas Embarcados
A análise cepstral — e, em particular, a interpretação do sinal no domínio da quefrequência — é uma das ferramentas mais poderosas e versáteis no processamento moderno de áudio. Seu ponto forte é justamente possibilitar a separação matemática e prática entre efeitos que, no domínio da frequência convencional, aparecem misturados de forma inseparável.
Ao longo deste artigo, vimos que:
- O cepstro transforma convoluções em somas através da operação log-espectral + IFFT.
- Esse processo reorganiza o conteúdo espectral, permitindo distinguir excitação, resposta acústica, pitch, ecos e timbre.
- A quefrequência interpreta periodicidades espectrais (não temporais), revelando padrões profundos do sinal.
- Em voz, permite separar fonte–filtro e detectar frequência fundamental mesmo sob ruído ou filtragem.
- Em instrumentação, auxilia na detecção de defeitos, ecos estruturais, vibrações periódicas e assinaturas mecânicas.
- Em classificação de eventos acústicos, os primeiros coeficientes cepstrais são extremamente eficientes — compactos, robustos e amigáveis para algoritmos embarcados.
Do ponto de vista de implementação embarcada:
- A análise cepstral é inteiramente viável no ESP32-P4, graças às instruções DSP nativas e ao suporte da biblioteca ESP-DSP.
- Um pipeline típico com janelas de 1024 amostras pode ser processado em tempo real com folga, mesmo associado a I2S + DMA.
- O código apresentado pode servir como base para:
- Detecção de voz (VAD);
- Estimativa de pitch;
- Extração de coeficientes cepstrais para classificadores;
- Estudo de reverberações e ecos;
- Detecção de falhas mecânicas via áudio/vibração.
A análise cepstral é especialmente adequada para sistemas embarcados modernos que precisam extrair significado de sinais sonoros complexos, mantendo consumo moderado de memória e CPU. Ela combina rigor matemático, elegância teórica e elevada eficiência prática — por isso permanece um dos pilares do processamento de áudio desde os anos 1960 até hoje.