O Desafio de Equilibrar um Equipamento com Duas Rodas

Equilibrar um equipamento sobre duas rodas, como um robô autoestabilizante (inspirado no famoso Segway), é uma tarefa complexa e instigante dentro do universo da robótica móvel. Ao contrário de veículos com três ou quatro rodas, que possuem estabilidade estática, um sistema com apenas duas rodas exige controle dinâmico contínuo para se manter na vertical. Isso ocorre porque seu centro de massa está acima do ponto de apoio (as rodas), formando um sistema inerentemente instável que se comporta como um pêndulo invertido.

Esse desafio é abordado utilizando sensores para medir o estado atual do sistema (como inclinação e velocidade angular), atuadores para aplicar forças corretivas (como motores DC ou brushless com controle PWM), e um algoritmo de controle de loop fechado que ajusta continuamente os comandos para manter o equilíbrio. O objetivo é detectar desvios do equilíbrio vertical e aplicar correções na direção e intensidade adequadas para restaurar o alinhamento.

Sensores Comuns Utilizados

• IMU (Unidade de Medição Inercial): Contém acelerômetro (mede aceleração linear) e giroscópio (mede velocidade angular). Alguns modelos também incluem magnetômetro.
• Encoder nos Motores: Para medir a rotação das rodas e estimar a velocidade do deslocamento.
• Sensor de Ultrassom ou ToF (opcional): Pode ser usado para evitar obstáculos ou medir distância do chão, mas não é necessário para o equilíbrio.

Atuadores Comuns Utilizados

• Motores DC ou Brushless com controle PWM: Conectados a um driver de potência, como L298N, VNH5019, ou drivers MOSFETs.
• Placa de controle (microcontrolador): Tipicamente um STM32, ESP32, Arduino ou Raspberry Pi.

Aplicações Práticas

Equipamentos de duas rodas autoequilibrantes podem ser usados em:

• Robôs de entrega ou vigilância.
• Cadeiras de rodas inteligentes.
• Plataformas móveis autônomas.
• Brinquedos ou dispositivos educacionais.

O domínio deste controle é um excelente exercício para estudar sistemas de controle de tempo real, fusão de sensores e algoritmos matemáticos aplicados a sistemas físicos.

Fundamentos Teóricos e Algoritmo de Controle

1. O Pêndulo Invertido: Modelagem Física

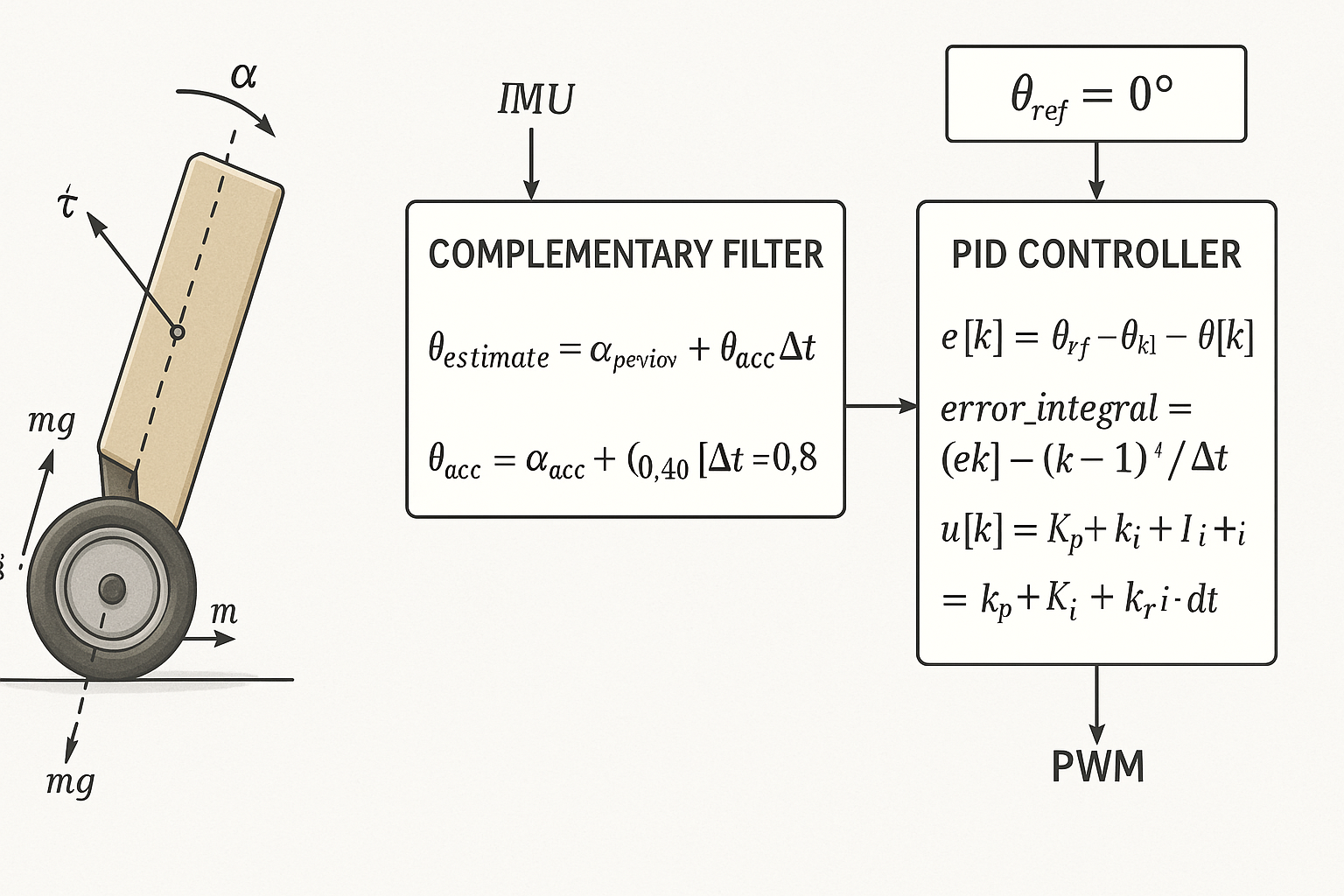
O comportamento de um robô de duas rodas é matematicamente semelhante a um pêndulo invertido. Quando a estrutura do robô se inclina para frente ou para trás, a gravidade gera um torque que o faz cair, exigindo uma ação ativa do motor para restaurar o equilíbrio.

A equação que governa o pêndulo invertido com base em torque é derivada das leis de Newton e pode ser escrita como:

\[
\tau = I \cdot \alpha = m \cdot g \cdot l \cdot \sin(\theta)
\]

Onde:

• τ = torque aplicado
• I = momento de inércia do sistema
• α = aceleração angular
• m = massa da estrutura
• g = aceleração da gravidade
• ll = distância do centro de massa ao ponto de rotação
• θ = ângulo de inclinação em relação à vertical

Para manter o equilíbrio, o sistema precisa aplicar torque (via motor) em resposta ao desvio angular θ, de forma a gerar uma aceleração que compense a tendência de queda.

2. Fusão Sensorial: Filtro Complementar

Sensores IMU fornecem dois tipos de medidas:

• O acelerômetro detecta o ângulo de inclinação, mas é sensível a ruído e vibrações.
• O giroscópio detecta a velocidade angular com boa precisão, mas sofre de drift (desvio acumulado com o tempo).

O filtro complementar combina os dois sensores para obter um ângulo mais estável:

\[
\theta_{\text{estimado}} = \alpha \cdot (\theta_{\text{anterior}} + \omega \cdot \Delta t) + (1 – \alpha) \cdot \theta_{\text{acc}}
\]

Onde:

• ω = velocidade angular do giroscópio
• θacc = ângulo estimado pelo acelerômetro
• α = coeficiente de mistura (tipicamente entre 0.90 e 0.98)
• Δt = tempo entre amostras

Esse filtro suaviza os dados e mantém uma estimativa confiável da inclinação.

3. Controle PID: Algoritmo de Feedback

O PID é um controlador de malha fechada que calcula a força de correção com base em três componentes:

• Proporcional (P): Corrige proporcionalmente ao erro atual.
• Integral (I): Corrige erros acumulados ao longo do tempo.
• Derivativo (D): Reage à taxa de variação do erro.

A equação do PID contínuo é:

\[
u(t) = K_p \cdot e(t) + K_i \cdot \int e(t)\,dt + K_d \cdot \frac{de(t)}{dt}
\]

Na forma discreta, para ser usada em código C:

\[
\begin{align*} e[k] &= \theta_{\text{ref}} – \theta[k] \\ \text{erro\_integral} &= \text{erro\_integral} + e[k] \cdot \Delta t \\ \text{erro\_derivada} &= \frac{e[k] – e[k-1]}{\Delta t} \\ u[k] &= K_p \cdot e[k] + K_i \cdot \text{erro\_integral} + K_d \cdot \text{erro\_derivada} \end{align*}
\]

Onde:

• u[k] = sinal de controle (PWM do motor)
• θref = posição desejada (em geral 0°, ou vertical)
• e[k] = erro no instante atual
• Δt = tempo entre atualizações (período da amostragem)

A saída do PID é então convertida em um comando PWM aplicado ao motor, movimentando o robô para corrigir a inclinação.

Código de Implementação

A seguir está uma versão simplificada do controlador de equilíbrio para um robô de duas rodas. O código assume que já há uma função para ler os dados da IMU e enviar sinais PWM para os motores.

1. Definições e Variáveis Globais

#define DT 0.01  // Intervalo de amostragem em segundos (10ms)
#define ALPHA 0.98  // Coeficiente do filtro complementar

// Constantes do PID
float Kp = 35.0;
float Ki = 0.5;
float Kd = 0.8;

// Variáveis do PID
float error = 0, previous_error = 0;
float integral = 0, derivative = 0;
float control_signal = 0;

// Variáveis do filtro complementar
float angle_gyro = 0;
float angle_acc = 0;
float angle = 0;  // Ângulo estimado final

2. Função para Atualização do Ângulo com Filtro Complementar

void atualizar_angulo(float acc_y, float acc_z, float gyro_x) {
    // Estimativa de inclinação a partir do acelerômetro (em graus)
    angle_acc = atan2(acc_y, acc_z) * 180 / 3.14159;

    // Integração da velocidade angular do giroscópio
    angle_gyro += gyro_x * DT;

    // Fusão dos sensores
    angle = ALPHA * angle_gyro + (1 - ALPHA) * angle_acc;
}

3. Função de Controle PID

void controle_PID(float setpoint) {
    error = setpoint - angle;
    integral += error * DT;
    derivative = (error - previous_error) / DT;

    control_signal = Kp * error + Ki * integral + Kd * derivative;

    previous_error = error;

    aplicar_PWM(control_signal);  // Envia o sinal para os motores
}

4. Laço Principal de Controle

void loop_de_controle() {
    float acc_y, acc_z, gyro_x;

    // 1. Ler sensores da IMU
    ler_IMU(&acc_y, &acc_z, &gyro_x);  // Função hipotética de leitura

    // 2. Atualizar ângulo estimado
    atualizar_angulo(acc_y, acc_z, gyro_x);

    // 3. Controlar com PID para manter posição vertical (0 graus)
    controle_PID(0.0);

    // 4. Esperar próximo ciclo
    delay_ms(DT * 1000);
}

Observações Importantes

• Leitura da IMU: a função ler_IMU() deve ser adaptada ao seu hardware. A maioria dos sensores como MPU6050 usam I2C.
• Saturação do PWM: é importante limitar o valor de control_signal para evitar sobrecarga nos motores (ex: clamp entre -255 e +255).
• Direção dos motores: valores positivos e negativos devem acionar os motores em sentidos opostos.
• Calibração: os valores de Kp, Ki, Kd devem ser ajustados empiricamente (tuning) para cada robô, podendo-se usar técnicas como Ziegler–Nichols ou tentativa e erro.