Quaternions
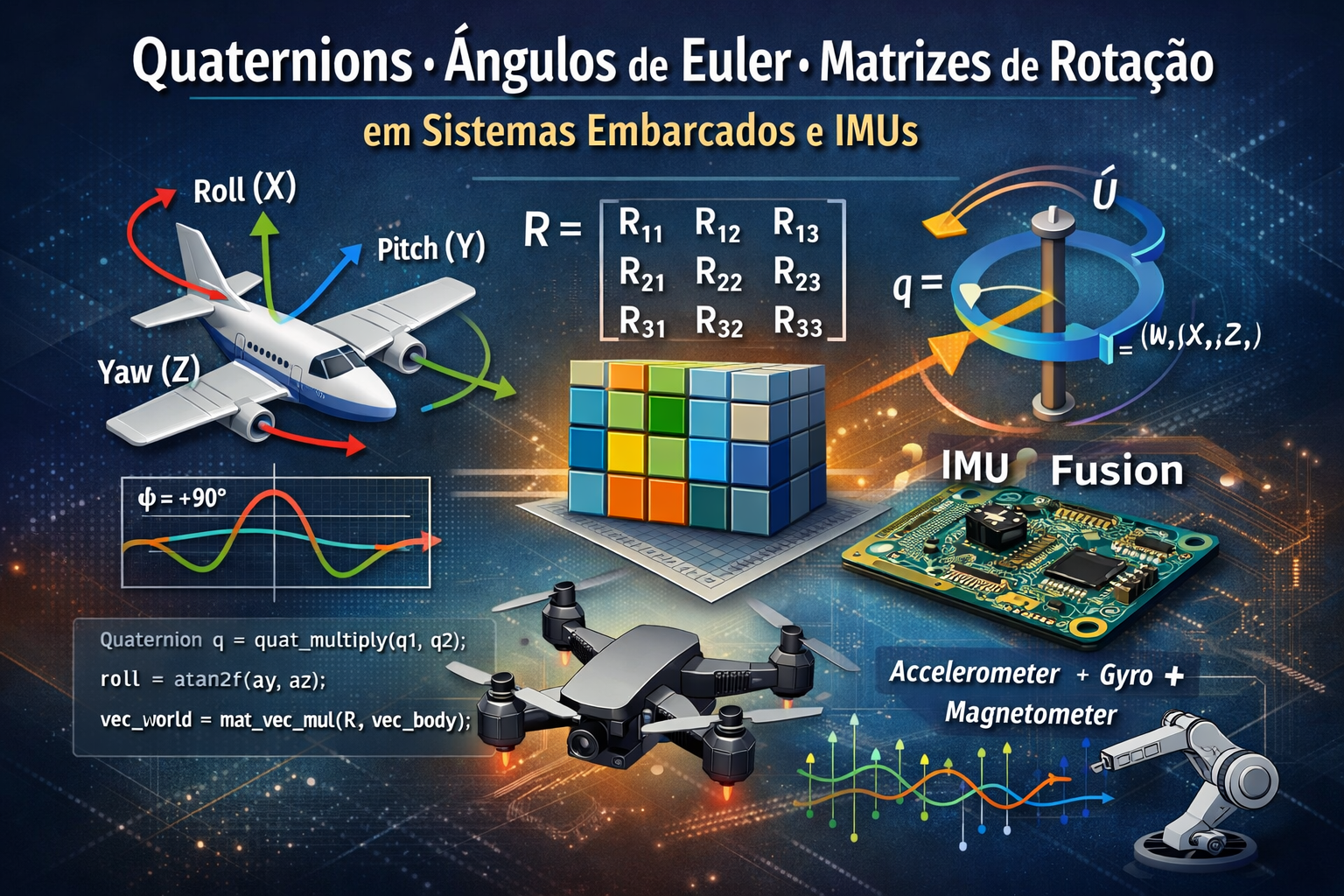
Quaternions são uma extensão dos números complexos introduzida por William Rowan Hamilton no século XIX, mas ganharam protagonismo real com a computação gráfica, robótica, navegação inercial e sistemas embarcados. Em vez de representar rotação como três ângulos sequenciais ou como uma matriz 3×3, o quaternion descreve uma rotação como uma entidade única composta por quatro componentes: uma parte escalar e uma parte vetorial.
Um quaternion é geralmente escrito como:
q = w + xi + yj + zk
ou, em forma vetorial:
q = (w, x, y, z)
Para aplicações de orientação, usamos quaternions unitários, isto é, aqueles cuja norma é igual a 1. A interpretação geométrica é elegante: um quaternion unitário representa uma rotação de ângulo θ em torno de um eixo unitário u = (ux, uy, uz). Nesse caso:
w = cos(θ/2)
x = ux * sin(θ/2)
y = uy * sin(θ/2)
z = uz * sin(θ/2)
Perceba algo importante: o ângulo aparece dividido por 2. Isso é consequência da álgebra dos quaternions e é o que permite evitar singularidades como o gimbal lock.
Representação em C
Vamos começar com uma estrutura simples:
#include <math.h>
#include <stdio.h>
/**
* @brief Estrutura para quaternion.
*/
typedef struct
{
float w; // Parte escalar
float x; // Parte vetorial X
float y; // Parte vetorial Y
float z; // Parte vetorial Z
} Quaternion;
Normalização
Para que o quaternion represente apenas rotação, ele deve ser unitário. Em sistemas embarcados, após integrações sucessivas do giroscópio, a normalização periódica é essencial.
/**
* @brief Normaliza um quaternion para norma unitária.
*/
Quaternion quat_normalize(Quaternion q)
{
float norm = sqrtf(q.w*q.w + q.x*q.x + q.y*q.y + q.z*q.z);
q.w /= norm;
q.x /= norm;
q.y /= norm;
q.z /= norm;
return q;
}
Multiplicação de Quaternions
A composição de rotações é feita por multiplicação de quaternions. Se q1 representa uma rotação e q2 outra, então a rotação composta é:
q = q1 ⊗ q2
A multiplicação não é comutativa. A ordem importa.
/**
* @brief Multiplica dois quaternions (q1 ⊗ q2).
*/
Quaternion quat_multiply(Quaternion q1, Quaternion q2)
{
Quaternion result;
result.w = q1.w*q2.w - q1.x*q2.x - q1.y*q2.y - q1.z*q2.z;
result.x = q1.w*q2.x + q1.x*q2.w + q1.y*q2.z - q1.z*q2.y;
result.y = q1.w*q2.y - q1.x*q2.z + q1.y*q2.w + q1.z*q2.x;
result.z = q1.w*q2.z + q1.x*q2.y - q1.y*q2.x + q1.z*q2.w;
return result;
}
Integração com Giroscópio
O giroscópio fornece velocidade angular ω = (ωx, ωy, ωz) em rad/s. Para integrar orientação, usamos a equação diferencial:
dq/dt = 0.5 * q ⊗ ωq
onde ωq é o quaternion puro (0, ωx, ωy, ωz).
Em implementação discreta com passo Δt:
q_new ≈ q + dq/dt * Δt
Exemplo simplificado:
/**
* @brief Atualiza quaternion usando dados do giroscópio.
*
* @param q Quaternion atual
* @param gx Velocidade angular eixo X (rad/s)
* @param gy Velocidade angular eixo Y
* @param gz Velocidade angular eixo Z
* @param dt Intervalo de tempo (s)
*/
Quaternion quat_update_gyro(Quaternion q, float gx, float gy, float gz, float dt)
{
Quaternion omega = {0.0f, gx, gy, gz};
Quaternion dq = quat_multiply(q, omega);
dq.w *= 0.5f;
dq.x *= 0.5f;
dq.y *= 0.5f;
dq.z *= 0.5f;
// Integração explícita
q.w += dq.w * dt;
q.x += dq.x * dt;
q.y += dq.y * dt;
q.z += dq.z * dt;
// Normaliza para evitar deriva numérica
return quat_normalize(q);
}
Esse é o núcleo matemático usado em filtros como Madgwick e Mahony, que adicionam termos de correção usando acelerômetro e magnetômetro.
Conversão para Ângulos de Euler
Apesar de trabalharmos internamente com quaternions, muitas aplicações precisam de roll, pitch e yaw.
/**
* @brief Converte quaternion para ângulos de Euler (Z-Y-X).
*/
void quat_to_euler(Quaternion q, float *roll, float *pitch, float *yaw)
{
// Roll (X)
*roll = atan2f(2.0f*(q.w*q.x + q.y*q.z),
1.0f - 2.0f*(q.x*q.x + q.y*q.y));
// Pitch (Y)
float sinp = 2.0f*(q.w*q.y - q.z*q.x);
if (fabsf(sinp) >= 1)
*pitch = copysignf(M_PI/2, sinp);
else
*pitch = asinf(sinp);
// Yaw (Z)
*yaw = atan2f(2.0f*(q.w*q.z + q.x*q.y),
1.0f - 2.0f*(q.y*q.y + q.z*q.z));
}
Note que aqui o problema do gimbal lock ainda pode aparecer na conversão, mas não na representação interna.
Vantagens Críticas dos Quaternions
Eles não sofrem gimbal lock na representação interna. Usam apenas quatro variáveis, são numericamente estáveis quando normalizados e permitem interpolação suave (SLERP), muito usada em controle de atitude e animação.
Em microcontroladores, especialmente Cortex-M4, M7 ou mesmo RP2040, a carga computacional é perfeitamente aceitável, principalmente se utilizarmos FPU (Unidade de Ponto Flutuante) ou otimizações com ponto fixo quando necessário.