A trigonometria esférica é um ramo da matemática que estuda relações entre ângulos e lados de triângulos definidos sobre a superfície de uma esfera. Diferente da trigonometria plana, onde os triângulos estão restritos ao plano euclidiano, a trigonometria esférica é essencial para problemas envolvendo navegação, astronomia e geolocalização por GPS, pois a Terra pode ser aproximada como uma esfera.
Nesse contexto, as Regras de Napier (Napier’s Rules), criadas por John Napier no século XVII, surgem como um conjunto de regras mnemônicas que simplificam a resolução de triângulos esféricos retos — aqueles que possuem um ângulo de 90°. Essas regras permitem relacionar diretamente os lados e ângulos de um triângulo esférico sem a necessidade de memorizar fórmulas extensas, funcionando como um método prático e elegante para cálculos de navegação.
Do ponto de vista histórico, a aplicação das Regras de Napier foi um avanço fundamental para a navegação marítima e astronômica. Antes da era digital, marinheiros e astrônomos dependiam dessas relações para calcular posições no globo terrestre a partir de observações de estrelas ou coordenadas geográficas. Hoje, mesmo com a precisão dos sistemas de posicionamento global (GPS), os princípios matemáticos por trás dessas regras permanecem vitais, pois embasam os algoritmos de cálculo de distância, rumo (azimute) e conversão de coordenadas usadas em receptores modernos.
Em termos práticos, ao estudar a geolocalização, cada posição na Terra é expressa por latitude e longitude, formando um triângulo esférico com o polo norte e uma linha de referência. Assim, compreender as Regras de Napier não é apenas um exercício matemático, mas também uma forma de enxergar como navegação aérea, marítima e até os satélites de GPS utilizam relações trigonométricas para fornecer localizações com grande precisão.
Fundamentos Matemáticos — As Regras de Napier
Para compreender as Regras de Napier, precisamos primeiro definir o que é um triângulo esférico reto. Um triângulo esférico é formado pela interseção de três grandes círculos de uma esfera (por exemplo, meridianos e o equador da Terra). Quando um dos ângulos desse triângulo é de 90°, temos o caso especial que pode ser tratado pelas regras de Napier.
Representação do Triângulo Esférico Reto
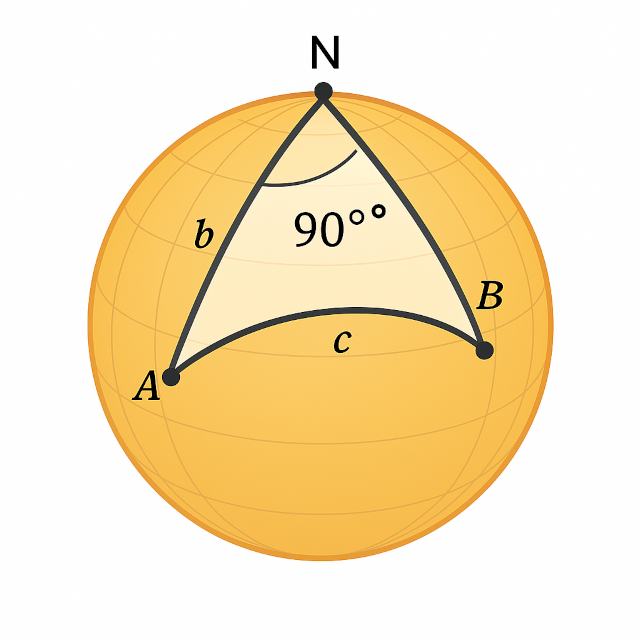
Imagine um triângulo esférico ABC na superfície da esfera:
- O ângulo em C é reto (C = 90°).
- Os lados são designados por letras minúsculas: a, b, c, onde cada lado é o arco oposto ao respectivo vértice.
- Assim: \[C‾a = \overline{BC}, b=AC‾b = \overline{AC}, c=AB‾c = \overline{AB}.\]
- Os ângulos são designados por letras maiúsculas: A, B, C.
Esse triângulo pode ser visualizado em cálculos de navegação, onde um vértice é o polo, outro é a posição de referência e o terceiro é a posição a ser calculada.
O Círculo de Napier
John Napier propôs um método gráfico conhecido como círculo de Napier:
- Colocamos em sequência cinco elementos do triângulo (os lados adjacentes ao ângulo reto e os dois ângulos agudos, mais o lado oposto ao ângulo reto).
- A ordem é:
\[A, \; b, \; C(=90°), \; a, \; B\]
- O ângulo reto (90°) é omitido, sobrando cinco elementos dispostos em círculo.
As Regras
Existem duas regras principais de Napier aplicáveis a esse círculo:
- A regra do elemento adjacente:
O seno de qualquer elemento é igual ao produto das tangentes dos dois elementos adjacentes. \(\sin(x) = \tan(y_1) \cdot \tan(y_2)\) - A regra do elemento oposto:
O seno de qualquer elemento é igual ao produto dos cossenos dos dois elementos opostos. \(\sin(x) = \cos(z_1) \cdot \cos(z_2)\)
Exemplo Didático
Suponha um triângulo esférico reto com:
- Ângulo A = 60°
- Ângulo B = 45°
Queremos calcular o lado c (oposto ao ângulo reto). Pela regra, temos: \[\cos(c) = \cos(a) \cdot \cos(b)\]
Mas como a e b estão relacionados a A e B, podemos usar as identidades derivadas de Napier para encontrar cada valor.
Essas fórmulas são a base para resolver problemas de navegação, como calcular a distância entre dois pontos dados em latitude e longitude.
Aplicação em Trigonometria Esférica
As Regras de Napier se destacam porque reduzem a complexidade de resolver triângulos esféricos retos a um conjunto simples de relações mnemônicas. Isso é extremamente útil em navegação, cartografia e sistemas de geolocalização, pois permite calcular distâncias, rumos e posições sem depender de métodos longos de interpolação.
Relações Fundamentais Derivadas das Regras
Para um triângulo esférico reto (C = 90°):
- Relação entre o lado oposto ao ângulo reto e os lados adjacentes:
\[\cos(c) = \cos(a) \cdot \cos(b)\]
- Relações envolvendo ângulos e lados:
\[\sin(a) = \sin(c) \cdot \sin(A) sin(b)=sin(c)⋅sin(B)\sin(b) = \sin(c) \cdot \sin(B)\]
- Relações para os ângulos agudos:
\[\cos(A) = \tan(b) \cdot \cot(c) cos(B)=tan(a)⋅cot(c)\cos(B) = \tan(a) \cdot \cot(c)\]
Essas expressões permitem resolver qualquer incógnita do triângulo conhecendo apenas parte dos lados ou ângulos.
Interpretação Geográfica
Na superfície da Terra, um triângulo esférico pode ser formado assim:
- O vértice C é o polo norte geográfico (ângulo reto).
- O lado a corresponde à colatitude do ponto A (\(90° – \varphi_A\)).
- O lado b corresponde à colatitude do ponto B (\(90° – \varphi_B)\).
- O ângulo C está sobre o polo, portanto mede a diferença de longitudes entre os dois pontos (\(\Delta \lambda)\).
- O lado c é a distância angular entre os pontos A e B sobre a esfera (grande círculo).
Assim, a relação: \(\cos(c) = \cos(a) \cdot \cos(b) + \sin(a) \cdot \sin(b) \cdot \cos(\Delta \lambda)\)
é diretamente aplicável ao cálculo da distância entre duas coordenadas GPS.
Exemplo de Uso
Se temos:
- Ponto A: latitude 40°N, longitude 10°W.
- Ponto B: latitude 20°N, longitude 30°W.
As colatitudes são: \(a = 90° – 40° = 50° b=90°−20°=70°b = 90° – 20° = 70°
A diferença de longitudes: \(\Delta \lambda = |30° – 10°| = 20°\)
Aplicando a fórmula: \(\cos(c) = \cos(50°) \cdot \cos(70°) + \sin(50°) \cdot \sin(70°) \cdot \cos(20°)\)
Isso nos dá o arco c, que multiplicado pelo raio da Terra (\(R \approx 6371\,km)\) fornece a distância entre os pontos.
Exemplos Práticos em Geolocalização
Agora que entendemos as fórmulas derivadas das Regras de Napier, podemos aplicá-las diretamente em cálculos de geolocalização. O caso clássico é determinar a distância entre dois pontos na Terra a partir de suas coordenadas GPS (latitude e longitude).
Fórmula Matemática
Dado dois pontos:
- \(P_1(\varphi_1, \lambda_1)\)
- \(P_2(\varphi_2, \lambda_2)\)
onde φ é a latitude e λ a longitude, a distância angular c entre eles é: \[\cos(c) = \sin(\varphi_1)\sin(\varphi_2) + \cos(\varphi_1)\cos(\varphi_2)\cos(\Delta \lambda)\]
onde: \[\Delta \lambda = \lambda_2 – \lambda_1\]
Finalmente, a distância real d é: \(d = R \cdot c\)
com \(R \approx 6371 \, \text{km}\) sendo o raio médio da Terra, e c expresso em radianos.
Exemplo Numérico
Ponto A: Fortaleza (\(\varphi_1 = -3.73°, \lambda_1 = -38.52°\))
Ponto B: Recife (\(\varphi_2 = -8.05°, \lambda_2 = -34.88°)\)
- Converter para radianos. \(\varphi_1 = -0.0651 \, rad, \quad \lambda_1 = -0.6722 \, rad\varphi_2 = -0.1405 \, rad, \quad \lambda_2 = -0.6087 \, rad\)
- Calcular \(\Delta \lambda\). \(\Delta \lambda = -0.6087 – (-0.6722) = 0.0635 \, rad\)
- Aplicar fórmula. \(\cos(c) = \sin(-0.0651)\sin(-0.1405) + \cos(-0.0651)\cos(-0.1405)\cos(0.0635) Resultado: c≈0.1334 radc \approx 0.1334 \, rad\)
- Distância: \(d = 6371 \cdot 0.1334 \approx 849 \, km\)
Essa é a distância em linha reta (grande círculo) entre Fortaleza e Recife.
Implementação em C
A seguir, um código simples para calcular a distância entre dois pontos GPS usando as regras de Napier:
#include <stdio.h>
#include <math.h>
// Raio médio da Terra em km
#define R 6371.0
// Função para converter graus em radianos
double deg2rad(double deg) {
return deg * M_PI / 180.0;
}
// Função que calcula a distância entre dois pontos GPS
double distanciaGPS(double lat1, double lon1, double lat2, double lon2) {
// Conversão para radianos
lat1 = deg2rad(lat1);
lon1 = deg2rad(lon1);
lat2 = deg2rad(lat2);
lon2 = deg2rad(lon2);
// Diferença de longitudes
double dlon = lon2 - lon1;
// Fórmula de Napier / Cosseno esférico
double cosc = sin(lat1) * sin(lat2) +
cos(lat1) * cos(lat2) * cos(dlon);
// Distância angular
double c = acos(cosc);
// Distância linear em km
return R * c;
}
int main() {
// Exemplo: Fortaleza -> Recife
double lat1 = -3.73, lon1 = -38.52;
double lat2 = -8.05, lon2 = -34.88;
double d = distanciaGPS(lat1, lon1, lat2, lon2);
printf("Distância: %.2f km\n", d);
return 0;
}
Explicação passo a passo:
- Conversão de graus para radianos: essencial porque funções trigonométricas em C (
sin,cos,acos) trabalham em radianos. - Aplicação da fórmula do cosseno esférico (derivada das Regras de Napier).
- Uso de
acospara obter a distância angular cc. - Multiplicação pelo raio da Terra para converter o arco em distância real.
Conclusão e Implicações Tecnológicas
As Regras de Napier, desenvolvidas no século XVII para simplificar cálculos de triângulos esféricos, continuam sendo uma das bases matemáticas mais relevantes para a navegação moderna. Embora hoje possamos contar com receptores GPS capazes de realizar milhões de operações por segundo, os princípios trigonométricos que sustentam esses cálculos permanecem os mesmos.
Na prática, os sistemas de navegação aérea e marítima, bem como aplicativos de geolocalização em smartphones, utilizam fórmulas derivadas da trigonometria esférica para determinar distâncias entre pontos na superfície da Terra, calcular rumos (azimutes) e corrigir trajetórias. Essas fórmulas estão embutidas em algoritmos que levam em conta a forma da Terra (aproximada por uma esfera ou elipsoide, como o WGS-84).
Outra implicação é no campo da aviação e defesa, onde a precisão dos cálculos esféricos é essencial para rotas intercontinentais e trajetórias de mísseis. Satélites de GPS, distribuídos em órbitas médias, também dependem da trigonometria esférica para calcular posições com margem de erro mínima.
Em um contexto tecnológico mais amplo, compreender as Regras de Napier ajuda engenheiros e programadores a desenvolverem sistemas embarcados otimizados para localização, evitando o uso de algoritmos pesados quando aproximações esféricas resolvem o problema de forma eficiente. Isso é particularmente útil em microcontroladores com recursos limitados, como em drones, robôs móveis e sensores remotos.
Portanto, embora inventadas em uma época em que cálculos eram feitos à mão com auxílio de tabelas, as Regras de Napier permanecem um elo entre a tradição matemática e as tecnologias de navegação do século XXI, garantindo que a geolocalização seja possível em qualquer escala — do smartphone ao sistema de controle de tráfego aéreo.