A trigonometria esférica é um ramo da matemática que trata das relações entre ângulos e lados de triângulos formados sobre a superfície de uma esfera. Diferentemente da trigonometria plana, que se aplica em superfícies bidimensionais, a trigonometria esférica lida com situações em que a curvatura não pode ser ignorada. Essa característica a torna essencial em aplicações práticas ligadas à navegação, geolocalização e guerra eletrônica, já que a Terra, as trajetórias de aeronaves e a orientação de antenas não podem ser reduzidas a meros planos.
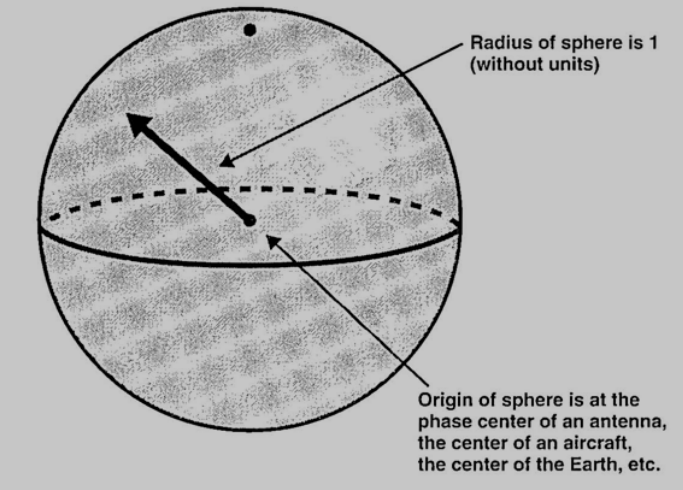
Um triângulo esférico é definido sobre uma esfera de raio unitário, ou seja, de raio igual a 1. Nesse modelo, o centro da esfera é colocado estrategicamente de acordo com o problema: no centro da Terra em cálculos de navegação, no centro da antena para problemas de direção de feixe (boresight), ou no centro de uma aeronave em cenários de engajamento. Os lados desse triângulo não são segmentos de reta, mas sim arcos de grandes círculos — círculos que resultam da interseção da esfera com planos que passam pelo seu centro. Os ângulos do triângulo, por sua vez, são os ângulos de interseção entre esses planos.
Essa construção, embora abstrata, reflete diretamente problemas do mundo real. Em navegação marítima, por exemplo, as rotas mais curtas entre dois pontos da superfície terrestre não são linhas retas em mapas, mas sim arcos de grandes círculos, conhecidos como ortodrômicas. Da mesma forma, em sistemas de radar, a orientação de uma antena é definida por ângulos de elevação e azimute, que nada mais são do que medidas derivadas de triângulos esféricos. Assim, compreender esses conceitos é fundamental para engenheiros que lidam com comunicação via satélite, sistemas de posicionamento global (GPS) e até mesmo algoritmos de direcionamento de armas guiadas.
Por fim, é importante destacar que nem todas as propriedades dos triângulos planos se mantêm em triângulos esféricos. Por exemplo, em um triângulo esférico é perfeitamente possível que os três ângulos internos sejam iguais a 90°, algo impossível na geometria euclidiana. Essas diferenças fundamentais abrem caminho para novas ferramentas matemáticas, essenciais para cálculos precisos em cenários complexos, onde ignorar a curvatura da esfera pode levar a erros significativos.
Conceitos Fundamentais
Para compreender os triângulos esféricos, é essencial começar pelo conceito de grande círculo. Em uma esfera, um grande círculo é qualquer círculo obtido pela interseção da superfície esférica com um plano que passa pelo centro da esfera. O Equador terrestre e os meridianos são exemplos clássicos de grandes círculos. Diferente de círculos menores, que não compartilham o mesmo centro da esfera, apenas os grandes círculos representam a menor distância entre dois pontos da superfície — uma propriedade usada tanto em navegação aérea e marítima quanto em cálculos de geolocalização.
Em um triângulo esférico, os “lados” não são segmentos de reta como em um triângulo plano, mas sim arcos de grandes círculos. Cada lado é definido pelo ângulo central formado entre os dois pontos extremos desse arco, medido no centro da esfera. Assim, os lados não têm comprimento linear em metros ou quilômetros, mas sim uma medida angular, geralmente em graus ou radianos. Esse detalhe é fundamental, pois mostra que o triângulo esférico é uma construção puramente angular, permitindo cálculos que independem do tamanho absoluto da esfera (seja ela o planeta Terra ou uma antena esférica).
Os ângulos internos de um triângulo esférico são formados pela interseção entre os planos que definem os grandes círculos. Essa definição pode parecer abstrata, mas pode ser visualizada facilmente em exemplos práticos. Imagine a Terra: se escolhermos o Polo Norte, o ponto de Greenwich (0° de longitude) no Equador e outro ponto no Equador a 90° de longitude leste, formamos um triângulo esférico cujos três ângulos internos medem 90°. Esse exemplo ilustra a principal diferença em relação à trigonometria plana: em um triângulo esférico, a soma dos ângulos internos sempre é maior que 180° e pode chegar a quase 540°.
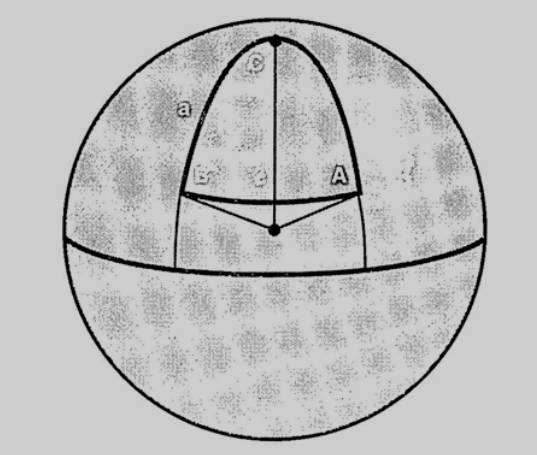
Para a notação, é comum usar letras minúsculas para representar os lados (a, b, c), que correspondem aos ângulos centrais associados a cada arco, e maiúsculas para os ângulos (A, B, C), sendo cada ângulo oposto ao lado com a mesma letra. Essa convenção facilita a aplicação das fórmulas clássicas da trigonometria esférica, como a lei dos senos esféricos e a lei dos cossenos esféricos, que serão exploradas em seções posteriores quando tratarmos de cálculos aplicados em navegação e posicionamento.
Outro ponto fundamental é a noção de excesso esférico. Enquanto em um triângulo plano a soma dos ângulos é exatamente 180°, em um triângulo esférico essa soma é maior, e a diferença entre o valor encontrado e 180° é chamada de excesso esférico. Esse excesso está diretamente relacionado à área do triângulo sobre a esfera e é um conceito essencial em cartografia e geodésia. Em resumo, os triângulos esféricos não apenas descrevem trajetórias e ângulos, mas também fornecem uma medida da própria superfície da esfera envolvida.
Aplicações Práticas
A utilidade dos triângulos esféricos vai muito além da teoria matemática; eles são ferramentas fundamentais em áreas como navegação, sistemas de posicionamento, comunicações via satélite e até mesmo em guerra eletrônica. Sempre que precisamos descrever direções, rotas ou ângulos sobre superfícies curvas, como a Terra ou a cúpula de radiação de uma antena, os triângulos esféricos fornecem a base de cálculo.
Na navegação marítima e aérea, por exemplo, o problema clássico é determinar a rota mais curta entre dois pontos na superfície terrestre. Essa rota é chamada de ortodrômica, que corresponde a um arco de grande círculo. Se um avião decolasse do Rio de Janeiro em direção a Tóquio, a trajetória mais curta não seria uma linha reta no mapa (loxodrômica), mas sim um arco que passa por latitudes bem mais altas, próximo ao Polo Norte. Para calcular esse percurso, a trigonometria esférica utiliza os lados e ângulos de triângulos formados entre o ponto de partida, o ponto de chegada e os polos da Terra.
No contexto dos sistemas de posicionamento global (GPS e similares), os triângulos esféricos aparecem quando se determina a posição de um receptor a partir dos sinais de múltiplos satélites. Cada satélite projeta sobre a Terra um conjunto de ângulos e distâncias que, quando tratados em conjunto, formam triângulos esféricos que permitem calcular latitude, longitude e até altitude com elevada precisão. Nesse caso, a trigonometria esférica é aliada da geometria tridimensional para transformar medidas de tempo (diferença de chegada do sinal) em coordenadas geográficas.
Já nas antenas e radares, os triângulos esféricos são indispensáveis para o cálculo de ângulos de apontamento. O ângulo de boresight, que define a direção central de emissão ou recepção da antena, é determinado a partir de ângulos de elevação e azimute, formando relações esféricas. Isso é crucial em aplicações militares, como em sistemas de rastreamento de mísseis, onde a precisão de frações de grau pode definir o sucesso de uma missão. De forma semelhante, em guerra eletrônica, quando duas aeronaves com velocidades diferentes em trajetórias arbitrárias interagem, a determinação de parâmetros como o deslocamento Doppler exige o uso de trigonometria esférica para modelar corretamente as direções relativas de movimento e radiação eletromagnética.
Por fim, em sistemas de armas guiadas, como mísseis antiaéreos, a determinação da trajetória de interceptação envolve resolver triângulos esféricos formados pela posição do lançador, do alvo e da trajetória prevista. Aqui, cada ângulo representa não apenas direções no espaço, mas também restrições de manobra e alcance. Isso demonstra como um conceito aparentemente abstrato se traduz em aplicações extremamente concretas e críticas, onde precisão matemática se converte em eficiência operacional.
Diferenças entre Triângulos Planos e Esféricos
Embora o conceito de triângulo seja familiar a todos, as diferenças entre o triângulo plano, estudado na geometria euclidiana, e o triângulo esférico, da trigonometria esférica, são profundas e afetam diretamente sua aplicação prática. A primeira e mais evidente distinção está na soma dos ângulos internos: em um triângulo plano, essa soma é sempre exatamente 180°, enquanto em um triângulo esférico ela é sempre maior que 180°, podendo chegar a quase 540°. Essa diferença ocorre porque os lados do triângulo esférico são arcos de grandes círculos, e não linhas retas, o que dá ao triângulo uma “curvatura” intrínseca.
Outra distinção fundamental é o conceito de lado. Em um triângulo plano, os lados são segmentos de reta com comprimento linear (em metros, quilômetros etc.). Já em um triângulo esférico, os lados são medidos como ângulos centrais (em graus ou radianos), que correspondem ao arco de um grande círculo. Assim, um lado de 90° em um triângulo esférico representa um quarto da circunferência da esfera, independentemente do tamanho absoluto dessa esfera. Essa propriedade permite aplicar os mesmos cálculos tanto em uma esfera terrestre quanto em uma esfera de dimensões muito menores, como no caso de antenas esféricas.
Além disso, há uma consequência direta: em um triângulo plano, não é possível que todos os ângulos internos sejam de 90°, pois isso violaria a soma fixa de 180°. No entanto, em um triângulo esférico isso é possível e até comum em exemplos didáticos. Se tomarmos o Polo Norte e dois pontos distintos no Equador, separados por 90° de longitude, formamos um triângulo esférico com três ângulos retos. Esse tipo de construção seria inconcebível na geometria plana, mas na esfera torna-se natural e útil para cálculos em navegação.
Outro ponto que diferencia os dois mundos é a relação com a área do triângulo. Em geometria plana, a área depende da base e da altura ou, de forma mais geral, das combinações de lados e ângulos. Já na trigonometria esférica, a área de um triângulo é diretamente proporcional ao seu excesso esférico — a diferença entre a soma dos ângulos internos e 180°. Isso cria uma conexão direta entre ângulos e área, algo inexistente em triângulos planos. Essa propriedade é explorada em geodésia e cartografia, pois permite medir áreas de regiões geográficas a partir de ângulos medidos em estações terrestres.
Portanto, enquanto os triângulos planos são adequados para problemas locais em pequenas escalas, os triângulos esféricos são indispensáveis em problemas globais ou espaciais, onde a curvatura da esfera não pode ser ignorada. Essa distinção não é apenas acadêmica, mas reflete a transição entre cálculos aproximados e cálculos de alta precisão em sistemas de posicionamento, defesa e comunicações.
Fórmulas Matemáticas da Trigonometria Esférica
Para que os conceitos de triângulos esféricos possam ser aplicados em navegação, guerra eletrônica e posicionamento, é fundamental conhecer as fórmulas que regem as relações entre seus lados e ângulos. Essas equações são equivalentes às leis da trigonometria plana, mas adaptadas ao espaço curvo da esfera.
1. Lei dos Senos Esféricos
A lei dos senos estabelece uma proporção entre os lados e ângulos de um triângulo esférico: \[\frac{\sin(a)}{\sin(A)} = \frac{\sin(b)}{\sin(B)} = \frac{\sin(c)}{\sin(C)}/]
Onde:
- a,b,ca, b, c são os lados (medidos como ângulos centrais, em graus ou radianos).
- A,B,CA, B, C são os ângulos internos opostos a cada lado.
Essa fórmula é amplamente usada em cálculos de navegação para determinar direções e distâncias angulares.
2. Lei dos Cossenos para os Lados
Permite relacionar os lados de um triângulo esférico com o cosseno do ângulo oposto: \[\cos(a) = \cos(b)\cos(c) + \sin(b)\sin(c)\cos(A)\]
Ciclicamente, as mesmas relações valem para os outros lados e ângulos.
3. Lei dos Cossenos para os Ângulos
Relaciona os ângulos internos com os lados correspondentes: cos(A)=−cos(B)cos(C)+sin(B)sin(C)cos(a)\cos(A) = -\cos(B)\cos(C) + \sin(B)\sin(C)\cos(a)
Essa equação é útil em situações em que se conhecem os lados e é necessário calcular os ângulos internos, como em rastreamento de antenas.
4. Excesso Esférico (Área do Triângulo)
A área de um triângulo esférico está ligada ao excesso angular EE: E=(A+B+C)−πE = (A + B + C) – \pi Aˊrea=E⋅R2\text{Área} = E \cdot R^2
Onde RR é o raio da esfera. Na esfera unitária (R=1R=1), a área é simplesmente igual ao excesso esférico.
5. Conversão para Coordenadas Cartesianas
Na prática, é comum converter coordenadas esféricas (latitude, longitude, raio) para cartesianas (x, y, z), especialmente em sistemas de navegação e processamento de sinais.
A conversão é feita pelas fórmulas: \[x = R \cdot \cos(\varphi) \cdot \cos(\lambda) y=R⋅cos(φ)⋅sin(λ)y = R \cdot \cos(\varphi) \cdot \sin(\lambda) z=R⋅sin(φ)z = R \cdot \sin(\varphi)\]
Onde:
- R é o raio da esfera (para cálculos teóricos, normalmente \(R=1\)).
- φ é a latitude (ângulo medido a partir do equador).
- λ é a longitude.
Essa transformação é essencial para integrar cálculos esféricos em sistemas computacionais, permitindo que dados de posicionamento (GPS, radares, antenas) sejam processados em modelos tridimensionais cartesianos.
6. Distância entre Dois Pontos na Esfera
A distância angular θ entre dois pontos \(\varphi_1, \lambda_1) e (φ2,λ2\varphi_2, \lambda_2) \)na esfera é dada por: \[\cos(\theta) = \sin(\varphi_1)\sin(\varphi_2) + \cos(\varphi_1)\cos(\varphi_2)\cos(\lambda_1 – \lambda_2)\]
A distância real é: \[d = R \cdot \theta\]
Essa é a fórmula usada em sistemas de navegação e geolocalização para calcular rotas e trajetórias entre cidades, aviões ou satélites.
Conclusão
Os triângulos esféricos representam uma poderosa ferramenta matemática para lidar com problemas em superfícies curvas, onde a geometria plana deixa de ser suficiente. Ao compreender como os lados são definidos por arcos de grandes círculos, como os ângulos se relacionam com planos que passam pelo centro da esfera e como as fórmulas específicas se aplicam, engenheiros e cientistas conseguem modelar situações complexas com precisão.
Em navegação, a trigonometria esférica garante que rotas marítimas e aéreas sejam calculadas de forma eficiente, utilizando trajetórias de grande círculo. Em sistemas de posicionamento global, como o GPS, permite converter medidas de tempo e sinais de satélite em coordenadas geográficas exatas. No campo das telecomunicações e da guerra eletrônica, possibilita determinar ângulos de boresight, orientar antenas e calcular efeitos Doppler em cenários de alta mobilidade. Até mesmo no controle de armas guiadas, sua aplicação é determinante para prever trajetórias de interceptação com elevado grau de acerto.
Comparados aos triângulos planos, os triângulos esféricos expandem nossa visão sobre as relações geométricas, introduzindo conceitos como o excesso esférico e a soma de ângulos superior a 180°. As fórmulas matemáticas que regem essas relações, associadas às conversões para coordenadas cartesianas, tornam-se pontes entre teoria e prática, permitindo a integração em sistemas embarcados e plataformas computacionais.
Portanto, compreender e aplicar a trigonometria esférica não é apenas um exercício acadêmico, mas uma necessidade real em um mundo cada vez mais dependente de sistemas de posicionamento, defesa e comunicação. É nesse encontro entre rigor matemático e aplicação prática que os triângulos esféricos revelam sua importância estratégica, tornando-se um dos pilares da engenharia moderna em contextos terrestres, marítimos, aéreos e espaciais.