Introdução à Programação Funcional
Apresentação do conceito e seu contraste com paradigmas tradicionais
A programação funcional é um paradigma que trata a computação como a avaliação de funções matemáticas, evitando mudanças de estado e dados mutáveis. Ao contrário do paradigma imperativo — que domina o desenvolvimento embarcado tradicional com C/C++ — a programação funcional favorece imutabilidade, funções puras e composição.
No contexto de sistemas embarcados, onde recursos são limitados e o controle sobre o tempo de execução é crucial, pode parecer contraintuitivo aplicar um estilo funcional. No entanto, quando corretamente adaptado, esse paradigma traz clareza, modularidade e testabilidade ao código embarcado — características valiosas em sistemas de missão crítica.
Vamos explorar ao longo deste artigo como é possível aplicar conceitos funcionais em linguagens imperativas como o C, e os benefícios dessa abordagem mesmo em ambientes com restrições como microcontroladores.
Princípios da Programação Funcional Adaptados ao C
Como aplicar os fundamentos funcionais em uma linguagem imperativa como o C
Apesar do C não ser uma linguagem funcional, é perfeitamente possível adaptar alguns dos princípios centrais desse paradigma para melhorar a clareza e a robustez do código em sistemas embarcados.
A seguir, explicamos como adaptar os principais conceitos:
🔁 Imutabilidade
Em vez de modificar variáveis globais ou estruturas diretamente, preferimos criar novas versões das estruturas ou atualizá-las de maneira controlada por função. Isso evita efeitos colaterais indesejados, principalmente em ambientes multitarefa ou com interrupções.
🧼 Funções puras
Uma função pura é aquela cujo resultado depende somente dos seus parâmetros e que não altera o estado global do sistema. Isso facilita testes, simulações e depuração.
🧩 Modularidade e composição
O código funcional tende a ser altamente modular. Pequenas funções são compostas para criar funções mais complexas, promovendo a reutilização e o desacoplamento de responsabilidades.
📌 Exemplo didático – Filtro de Média Móvel
Vamos analisar um exemplo de função pura implementando um filtro de média móvel sem estado global:
cCopiarEditartypedef struct {
float buffer[5];
int index;
int count;
} MovingAverageFilter;
float calculate_moving_average(const MovingAverageFilter* old, float new_val, MovingAverageFilter* updated) {
*updated = *old;
updated->buffer[updated->index] = new_val;
updated->index = (updated->index + 1) % 5;
if (updated->count < 5) updated->count++;
float sum = 0.0f;
for (int i = 0; i < updated->count; i++) sum += updated->buffer[i];
return sum / updated->count;
}
Esse estilo facilita o uso seguro do filtro mesmo em ambientes com multitarefa (como FreeRTOS), pois evita condições de corrida.
Aplicando Estilo Funcional ao Controle PID
Construindo um controlador robusto sem efeitos colaterais
O controle PID (Proporcional, Integral, Derivativo) é um dos algoritmos mais utilizados em sistemas embarcados para regulação de temperatura, velocidade, posição e muito mais. Tradicionalmente, sua implementação em C utiliza variáveis globais ou estruturas mutáveis. No entanto, ao aplicar o paradigma funcional, é possível obter um controlador mais previsível e modular.
🎯 Objetivo
Implementar um PID em que o estado interno (erro anterior e termo integral) seja gerenciado por estruturas imutáveis, e a função pid_compute() opere de forma pura, retornando a nova saída e o novo estado separadamente.
🧱 Estrutura do estado
cCopiarEditartypedef struct {
float kp, ki, kd;
float prev_error;
float integral;
float out_min, out_max;
} PIDState;
🧮 Função pid_compute (sem anti-windup por enquanto)
cCopiarEditarfloat pid_compute(const PIDState* state, float setpoint, float measured, float dt, PIDState* updated) {
float error = setpoint - measured;
float derivative = (error - state->prev_error) / dt;
*updated = *state; // cópia do estado anterior
updated->integral += error * dt;
updated->prev_error = error;
float output = (state->kp * error) +
(state->ki * updated->integral) +
(state->kd * derivative);
// Aplicar saturação
if (output > state->out_max) output = state->out_max;
if (output < state->out_min) output = state->out_min;
return output;
}
📍 Vantagens:
- Reentrância: várias instâncias de PID podem ser executadas em paralelo.
- Testabilidade: pode ser testado fora do hardware.
- Transparência: nenhuma variável global envolvida.
Na próxima seção, vamos expandir esse PID com uma técnica anti-windup por back-calculation, ainda mantendo o estilo funcional.
Anti-Windup com Back-Calculation em Estilo Funcional
Corrigindo o acúmulo excessivo da ação integral em sistemas com saturação
Nos sistemas de controle real, os atuadores possuem limites físicos: um motor, por exemplo, não pode girar mais rápido do que sua capacidade máxima. Quando a saída do controlador PID excede esses limites e o sistema continua acumulando o erro integral, ocorre o fenômeno conhecido como “windup”.
⚠️ Problema
Esse acúmulo leva a um retardo na recuperação da estabilidade, gerando overshoots e oscilações indesejadas mesmo após o erro ter sido corrigido.
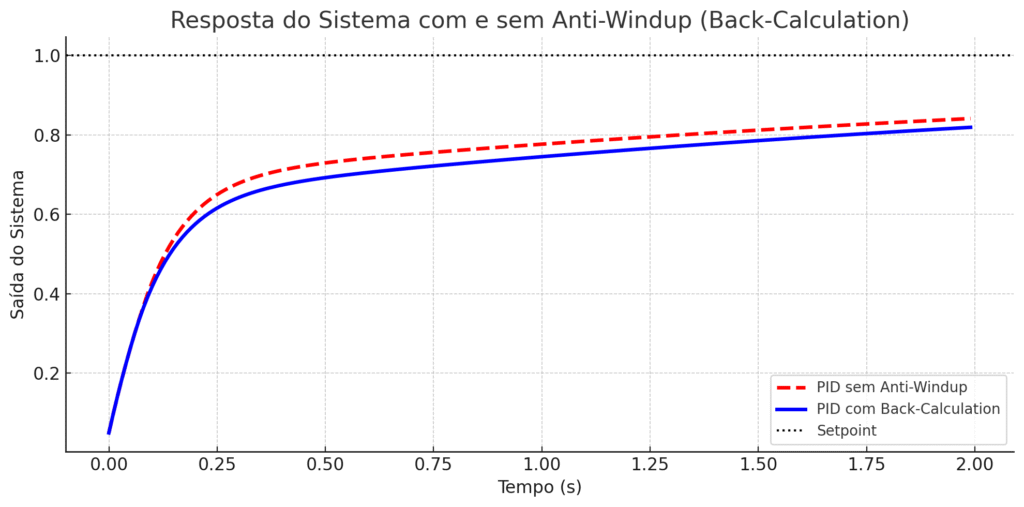
🛡️ Solução: Back-Calculation
O método de anti-windup por back-calculation realimenta o erro entre a saída calculada e a saída saturada de volta ao integrador, amortecendo o acúmulo com um ganho de correção k_aw.
🔧 Estado expandido:
cCopiarEditartypedef struct {
float kp, ki, kd;
float prev_error;
float integral;
float out_min, out_max;
float k_aw; // ganho de anti-windup
} PIDState;
🧠 Função pura com back-calculation:
cCopiarEditarfloat pid_compute(const PIDState* state, float setpoint, float measured, float dt, PIDState* updated) {
float error = setpoint - measured;
float derivative = (error - state->prev_error) / dt;
// Cálculo da saída antes da saturação
float u_unclamped = (state->kp * error) +
(state->ki * state->integral) +
(state->kd * derivative);
// Aplica saturação
float u_clamped = u_unclamped;
if (u_clamped > state->out_max) u_clamped = state->out_max;
if (u_clamped < state->out_min) u_clamped = state->out_min;
// Cópia e atualização de estado
*updated = *state;
float saturation_error = u_clamped - u_unclamped;
// Integra com back-calculation
updated->integral += (error + state->k_aw * saturation_error) * dt;
updated->prev_error = error;
return u_clamped;
}
📌 Nota sobre k_aw
Um valor típico é k_aw = 1/ki, mas isso pode variar de acordo com a planta controlada.
✅ Benefícios da abordagem funcional com anti-windup:
- Resposta mais rápida ao sair da saturação
- Menor overshoot e recuperação mais suave
- Controlador testável, seguro e desacoplado de estado global
Conclusão e Aplicações Práticas
Programação funcional como aliada da confiabilidade em sistemas embarcados
Ao longo deste artigo, demonstramos que, mesmo em linguagens imperativas como o C, é possível aplicar com sucesso os princípios da programação funcional em sistemas embarcados. Essa abordagem, quando bem aplicada, oferece ganhos importantes:
🎯 Benefícios observados
- Redução de efeitos colaterais, tornando o sistema mais previsível
- Facilidade de teste e simulação, ideal para ambientes críticos
- Reentrância e paralelismo seguros, especialmente quando usados com RTOS ou interrupções
- Manutenção simplificada, pois cada função é autocontida e independente de estado global
🔌 Aplicações práticas
- Controle de motores, como servos ou motores BLDC
- Regulação de temperatura, com controladores PID em sistemas HVAC ou aquecedores
- Filtragem digital de sinais, com filtros deslizantes, IIR ou FIR
- Interfaces sensoriais desacopladas, onde a lógica de leitura é separada da manipulação do dado
🚀 Um passo em direção à confiabilidade
Sistemas embarcados modernos estão cada vez mais complexos, conectados e críticos. A adoção de técnicas funcionais representa um passo estratégico para projetos que buscam robustez, verificabilidade e segurança — atributos essenciais para aplicações em aeronáutica, automação industrial, dispositivos médicos e IoT.
Na próxima seção, incluiremos um gráfico que ilustra visualmente os ganhos obtidos com o uso do anti-windup com back-calculation, comparado à versão sem esse recurso.