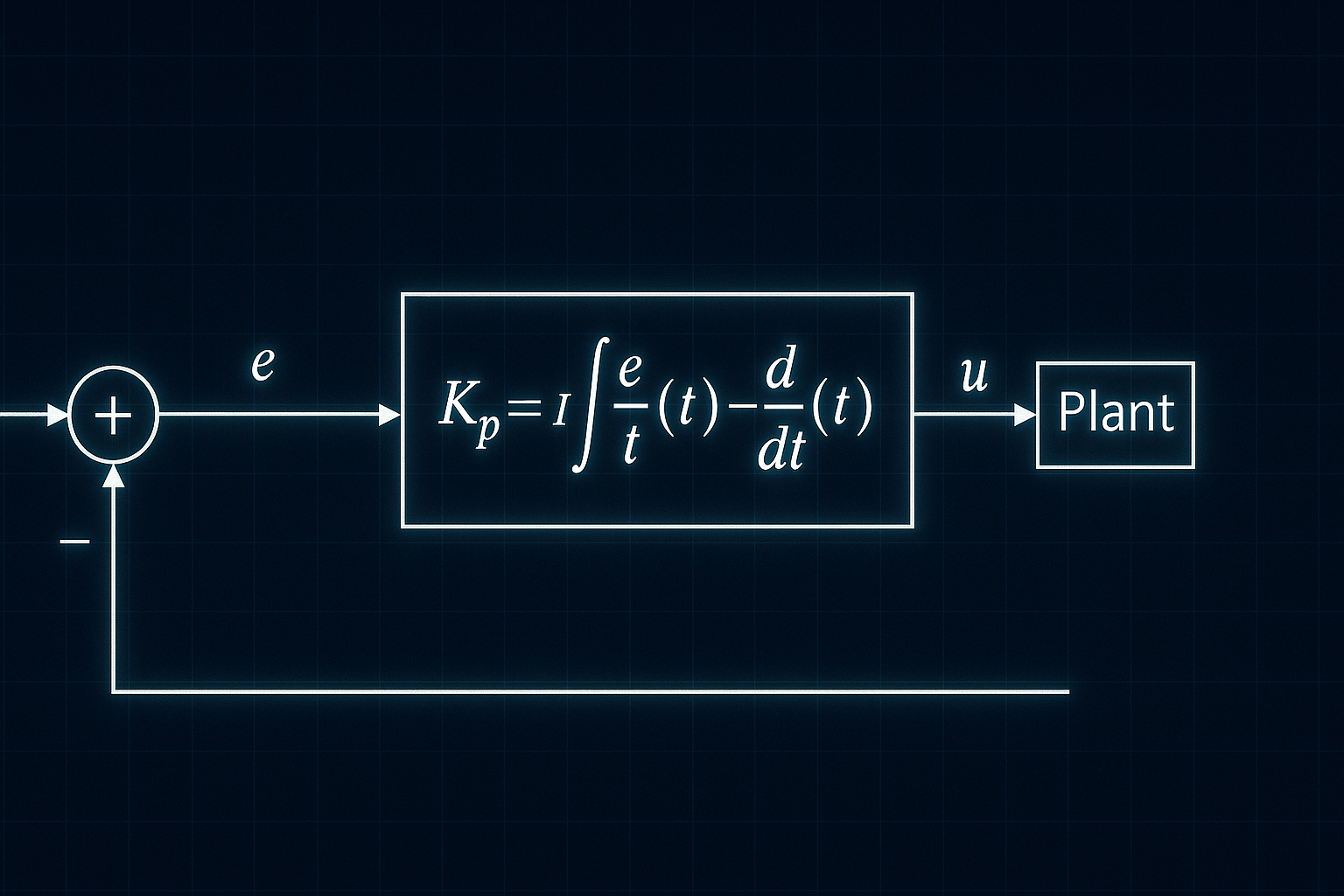PID na Prática: Fundamentos, Fórmulas, Simulação e Implementação em C para Sistemas Embarcados

Quando falamos em controle de sistemas (temperatura, velocidade de motor, posição de eixo, nível de tanque, etc.), a primeira grande divisão é entre malha aberta e malha fechada.

Malha aberta: você envia um comando para o sistema (planta) e não verifica se o resultado foi realmente o desejado.
Malha fechada (feedback): você mede a saída real, compara com o valor desejado (referência) e ajusta o comando com base nesse erro.

Do ponto de vista matemático, em malha fechada definimos três sinais fundamentais:

\( r(t) \) – referência ou setpoint (valor desejado: temperatura alvo, velocidade alvo, etc.);
\( y(t) \) – saída medida do sistema (sensor);
\( e(t) \) – erro, diferença entre o que queremos e o que estamos obtendo.

A relação básica é:

\[
e(t) = r(t) – y(t)
\]

O controlador (que pode estar implementado em C em um microcontrolador) recebe ( e(t) ) e gera o sinal de controle ( u(t) ) a ser aplicado na planta (por exemplo, PWM do motor, duty-cycle de uma fonte chaveada, corrente em uma resistência de aquecimento, etc.). Em forma de blocos:

\[
r(t) ; \xrightarrow{;\text{cálculo do erro};} e(t) \xrightarrow{;\text{controlador};} u(t) \xrightarrow{;\text{planta};} y(t)
\]

ou de forma resumida:

\[
u(t) = f\big(e(t)\big)
\]

O que transforma o simples “ligar/desligar” num sistema de controle mais sofisticado é justamente a escolha da função ( f(\cdot) ). O controlador PID (Proporcional–Integral–Derivativo) é uma forma específica e muito poderosa de definir essa função.

O que é o PID em termos intuitivos?

O PID é um controlador que combina três ações sobre o erro:

Proporcional (P) – reage ao tamanho atual do erro.
- Se o erro é grande, o controlador reage com uma ação de controle grande.
- É como alguém que empurra mais forte o carrinho quanto maior for a diferença até o alvo.
Integral (I) – observa o erro acumulado ao longo do tempo.
- Se o sistema fica “quase” no valor desejado, mas sempre com um pequeno erro, o termo integral vai somando esse erro e “empurrando” a saída até eliminar o erro em regime permanente.
Derivativo (D) – reage à velocidade de variação do erro.
- Se o erro está mudando rapidamente, o termo D tenta “frear” essa mudança, ajudando a reduzir os overshoots (quando a saída passa muito do valor desejado).

Na forma contínua, a equação geral do PID (no domínio do tempo) é:

\[
u(t) = K_p \cdot e(t) ;+; K_i \int_0^t e(\tau), d\tau ;+; K_d \cdot \frac{de(t)}{dt}
\]

onde:

\( K_p \) é o ganho proporcional;
\( K_i \) é o ganho integral;
\( K_d \) é o ganho derivativo.

Em palavras: o sinal de controle é soma ponderada de três componentes: um proporcional ao erro, um proporcional ao erro acumulado e um proporcional à taxa de variação do erro.

Por que o PID é tão usado?

O PID é extremamente popular em engenharia de controle (e em sistemas embarcados) por vários motivos:

É simples de entender conceitualmente;
É relativamente fácil de implementar em C em um microcontrolador;
Funciona muito bem para uma grande variedade de plantas de primeira e segunda ordem, mesmo quando não temos um modelo matemático super preciso do sistema;
Permite ajustar compromisso entre tempo de resposta, overshoot, estabilidade e erro em regime apenas mexendo em três parâmetros: \( K_p, K_i, K_d \).

Além disso, em muitos sistemas industriais e acadêmicos, o PID é a “primeira escolha”: se bem ajustado, resolve 80–90% dos casos típicos de controle de processo, motores, temperatura, nível, etc.

Controle em malha fechada simples x PID

Para entender a importância do PID, vale comparar com uma estratégia de controle bem mais simples: o controle “tudo ou nada” (on–off). Imagine um sistema de aquecimento com histerese:

// Exemplo C simples (controle on-off com histerese)
float setpoint = 50.0f;      // temperatura desejada (°C)
float hysteresis = 1.0f;     // banda morta
int   heater_on = 0;         // 0 = desligado, 1 = ligado

void control_loop(void) {
    float temp = read_temperature_sensor();  // mede a saída y(t)

    if (temp < (setpoint - hysteresis)) {
        heater_on = 1;       // liga o aquecedor
    } else if (temp > (setpoint + hysteresis)) {
        heater_on = 0;       // desliga o aquecedor
    }

    set_heater_output(heater_on);
}

// Exemplo C simples (controle on-off com histerese)
float setpoint = 50.0f;      // temperatura desejada (°C)
float hysteresis = 1.0f;     // banda morta
int   heater_on = 0;         // 0 = desligado, 1 = ligado

void control_loop(void) {
    float temp = read_temperature_sensor();  // mede a saída y(t)

    if (temp < (setpoint - hysteresis)) {
        heater_on = 1;       // liga o aquecedor
    } else if (temp > (setpoint + hysteresis)) {
        heater_on = 0;       // desliga o aquecedor
    }

    set_heater_output(heater_on);
}

Esse tipo de controle é:

Fácil de implementar;
Funciona “mais ou menos” bem para alguns sistemas lentos (como aquecimento).

Mas apresenta problemas típicos:

Oscilações em torno do setpoint (liga/desliga o tempo todo);
Pouco controle sobre tempo de subida, overshoot e estabilidade;
Difícil atender especificações mais rigorosas de desempenho.

O PID surge justamente como uma evolução desse conceito, trazendo uma ação contínua (não só 0 ou 1), permitindo gerar um comando suave entre, por exemplo, 0% e 100% de PWM, de forma proporcional e inteligente ao erro e à sua dinâmica.

Visão geral do que virá nas próximas seções

Ao longo do artigo vamos:

Modelar de forma simples uma planta (sistema controlado) para entender a resposta em malha fechada;
Derivar a equação do PID no tempo contínuo e no tempo discreto (para implementação em firmware);
Implementar um PID em C, passo a passo, primeiro em ponto flutuante, depois discutindo versões otimizadas (inteiros / fixed-point e anti-windup);
Comparar PID com outros tipos de controladores de malha fechada: P, PI, PD, on–off e estratégias mais avançadas;
Apresentar estratégias básicas de sintonia de ganhos ( K_p, K_i, K_d ) para iniciantes.

Modelagem Simples da Planta e Comportamento de Malha Fechada

Antes de mergulharmos no PID em si, é fundamental compreender a dinâmica da planta — isto é, o comportamento natural do sistema que desejamos controlar. Mesmo uma modelagem simples ajuda enormemente a entender por que certas configurações do PID funcionam bem e outras levam à instabilidade, oscilação ou lentidão excessiva.

1. O que é uma Planta em Controle?

Na engenharia de controle, planta é o nome dado ao sistema físico cujas variáveis queremos controlar. Pode ser:

A temperatura de um forno,
A velocidade de um motor DC,
A corrente em um conversor buck,
O ângulo de um servomecanismo,
A posição de um robô com STM32.

A planta sempre possui dinâmica, ou seja, a saída não muda instantaneamente quando aplicamos um comando.

2. Exemplo Didático: Planta de Primeira Ordem

Para iniciantes, o modelo mais simples e útil é a planta de primeira ordem. Ela representa sistemas onde a saída responde com atraso suave e gradual ao sinal de controle.

O modelo clássico é:

\[
\tau \frac{dy(t)}{dt} + y(t) = K \cdot u(t)
\]

onde:

\( y(t) \) — saída (velocidade, temperatura…)
\( u(t) \) — entrada (PWM, corrente…)
\( K \) — ganho da planta
\( \tau \) — constante de tempo (define a “lentidão” do sistema)

Esse modelo descreve:

Subidas exponenciais,
Respostas suaves sem overshoot,
Plantas estáveis que não oscilam sozinhas.

3. Solução do Modelo — Resposta ao Degrau

Se aplicarmos um degrau na entrada \( u(t) = U_0 \), a solução da equação diferencial é:

\[
y(t) = K U_0 \left(1 – e^{-t/\tau}\right)
\]

Explicação:

Quando o tempo aumenta, o termo ( e^{-t/\tau} ) vai a zero.
A saída tende ao valor de regime:

\[
y_{\text{reg}} = K \cdot U_0
\]

Após um tempo igual a ( \tau ), a planta atinge aproximadamente 63% do valor final.
Após 4τ, o sistema está praticamente estabilizado.

4. Planta Discreta (para implementação em C)

Em firmware, não lidamos com equações diferenciais contínuas, mas com valores amostrados a cada período de controle ( T_s ).

A versão discreta da planta de primeira ordem é:

\[
y[k] = a \cdot y[k-1] + b \cdot u[k]
\]

onde:

\( a = e^{-T_s/\tau} \)
\( b = K \left(1 – e^{-T_s/\tau}\right) \)

Esse modelo é extremamente útil para simular e testar controladores PID em C sem hardware real.

5. Exemplo em C — Simulação de uma Planta de Primeira Ordem

O exemplo abaixo calcula a resposta da planta ao longo do tempo e imprime a saída no terminal.

#include <stdio.h>
#include <math.h>

// Parâmetros da planta
#define K_PLANTA 1.0f
#define TAU      0.5f
#define TS       0.01f   // tempo de amostragem (10 ms)
#define STEPS    200     // número de iterações

int main() {
    float a = expf(-TS / TAU);
    float b = K_PLANTA * (1.0f - a);

    float y = 0.0f;   // saída da planta
    float u = 1.0f;   // degrau de entrada

    for (int k = 0; k < STEPS; k++) {
        y = a * y + b * u;
        printf("%d\t%.4f\n", k, y);
    }

    return 0;
}

#include <stdio.h>
#include <math.h>

// Parâmetros da planta
#define K_PLANTA 1.0f
#define TAU      0.5f
#define TS       0.01f   // tempo de amostragem (10 ms)
#define STEPS    200     // número de iterações

int main() {
    float a = expf(-TS / TAU);
    float b = K_PLANTA * (1.0f - a);

    float y = 0.0f;   // saída da planta
    float u = 1.0f;   // degrau de entrada

    for (int k = 0; k < STEPS; k++) {
        y = a * y + b * u;
        printf("%d\t%.4f\n", k, y);
    }

    return 0;
}

Ao rodar o código, a saída exibirá uma curva crescente típica de um sistema de primeira ordem.

6. O que Você Deve Perceber Dessa Seção

Uma planta de primeira ordem é lenta e suave — ótima para aprender controle.
O tempo de resposta depende da constante ( \tau ).
Plantas reais podem ser mais complexas (2ª ordem, com atrito, com atraso de transporte etc.).
Mesmo assim, começamos com modelos simples para entender o comportamento fundamental.

Derivação Completa do Controlador PID (Contínuo e Discreto)

Agora que já estabelecemos o que é a planta e como o erro ( e(t) ) se relaciona com o sinal de controle, vamos derivar cuidadosamente o PID contínuo e a sua forma discreta, que é a usada em microcontroladores.

Esta seção é fundamental: aqui você aprende de onde vêm as fórmulas, por que elas funcionam e como traduzir tudo isso para C de forma segura e eficiente.

1. Revisão Intuitiva das Três Ações

O controlador PID é definido pela soma de três componentes:

Proporcional (P)
Integral (I)
Derivativo (D)

Cada uma reage ao erro de uma forma distinta:

\[
u(t) = u_P(t) + u_I(t) + u_D(t)
\]

onde:

\( u_P(t) = K_p \cdot e(t) \)
\( u_I(t) = K_i \cdot \int_0^t e(\tau), d\tau \)
\( u_D(t) = K_d \cdot \frac{de(t)}{dt} \)

Essa é a forma contínua, idealizada.

Mas no firmware, nada é contínuo — tudo é amostrado.

2. Forma Contínua do PID

A expressão tradicional é:

\[
u(t) = K_p e(t) + K_i \int_0^t e(\tau), d\tau + K_d \frac{de(t)}{dt}
\]

Essa formulação:

É matematicamente elegante;
Ajuda no projeto teórico;
Não pode ser usada diretamente em C, pois integra e deriva continuamente.

Para converter para o uso real, precisamos discretizar.

3. Discretização do PID (Amostragem)

3.1 Erro discreto

O controlador roda a cada período de amostragem ( T_s ). Então definimos:

\[
e[k] = r[k] – y[k]
\]

onde ( k ) é o índice da iteração.

4. Ação Proporcional (discreta)

Simplesmente:

\[
u_P[k] = K_p \cdot e[k]
\]

Essa parte é direta — basta multiplicar.

5. Ação Integral (discreta)

A integral é a soma acumulada dos erros:

\[
u_I[k] = u_I[k-1] + K_i \cdot T_s \cdot e[k]
\]

onde:

\( u_I[k] \) é o valor integral acumulado,
O termo \( K_i \cdot T_s \) costuma ser chamado de ganho integral discreto.

Esse termo é responsável por eliminar o erro de regime permanente.

Mais adiante trataremos do problema do windup, ou “saturação integral”.

6. Ação Derivativa (discreta)

Usamos uma derivada numérica simples:

\[
u_D[k] = K_d \cdot \frac{e[k] – e[k-1]}{T_s}
\]

Se quisermos uma forma mais filtrada (menos ruidosa), podemos implementar um filtro passa-baixa — veremos depois.

7. Fórmula Completa do PID Discreto

Somando P, I e D:

\[
u[k] = K_p e[k] ;+; u_I[k] ;+; K_d \frac{e[k] – e[k-1]}{T_s}
\]

Essa é a forma mais direta para firmware.

8. Implementação do PID Discreto — Versão Didática em C

Aqui está o código mais claro possível para iniciantes.

typedef struct {
    float Kp;
    float Ki;
    float Kd;

    float Ts;          // tempo de amostragem

    float integrator;   // acumulo integral
    float prev_error;   // erro da iteração anterior
    float prev_output;  // saída anterior (opcional)
} PID_Controller;

float PID_Update(PID_Controller *pid, float setpoint, float measurement) {
    // 1. Calcula erro
    float error = setpoint - measurement;

    // 2. Termo proporcional
    float P = pid->Kp * error;

    // 3. Termo integral
    pid->integrator += pid->Ki * pid->Ts * error;
    float I = pid->integrator;

    // 4. Termo derivativo
    float derivative = (error - pid->prev_error) / pid->Ts;
    float D = pid->Kd * derivative;

    // 5. Soma dos termos
    float output = P + I + D;

    // 6. Atualiza estado
    pid->prev_error = error;
    pid->prev_output = output;

    return output;
}

typedef struct {
    float Kp;
    float Ki;
    float Kd;

    float Ts;          // tempo de amostragem

    float integrator;   // acumulo integral
    float prev_error;   // erro da iteração anterior
    float prev_output;  // saída anterior (opcional)
} PID_Controller;

float PID_Update(PID_Controller *pid, float setpoint, float measurement) {
    // 1. Calcula erro
    float error = setpoint - measurement;

    // 2. Termo proporcional
    float P = pid->Kp * error;

    // 3. Termo integral
    pid->integrator += pid->Ki * pid->Ts * error;
    float I = pid->integrator;

    // 4. Termo derivativo
    float derivative = (error - pid->prev_error) / pid->Ts;
    float D = pid->Kd * derivative;

    // 5. Soma dos termos
    float output = P + I + D;

    // 6. Atualiza estado
    pid->prev_error = error;
    pid->prev_output = output;

    return output;
}

Essa é a base do PID clássico.

9. O que você deve entender desta seção

O PID contínuo não é diretamente programável: precisamos transformá-lo em uma versão discreta.
A discretização envolve aproximação da integral com soma acumulada e da derivada com diferença entre amostras.
O resultado é um algoritmo simples, rápido e adequado para microcontroladores de 8, 16 ou 32 bits.
Esta é a fundação para versões mais robustas: anti-windup, saturação, derivada filtrada, PID em ponto fixo, etc.

Implementação Completa do PID em C

(com Saturação, Anti-Windup, Derivada Filtrada e Estrutura Robusta)

Nesta seção avançamos da versão didática do PID para uma implementação realista, própria para sistemas embarcados. A ideia é construir um controlador seguro, estável e pronto para produção em microcontroladores ARM Cortex-M, RISC-V, AVR ou RP2040.

Vamos abordar:

Saturação da saída
Anti-windup (evita integral descontrolada)
Derivada filtrada (reduz ruído)
Proteção contra valores inválidos
Versão final robusta

1. Saturação da Saída (Clamping)

Em sistemas reais, a saída do controle nunca é ilimitada. Exemplos:

PWM entre 0% e 100%
Corrente máxima limitada
Ângulo de servo limitado
Tensão restrita

Para evitar comandos fisicamente impossíveis, fazemos:

\[
u_{\text{sat}} = \min(\max(u,, u_{\min}),, u_{\max})
\]

Se ignorarmos isso, o controlador pode gerar valores absurdos e tornar o sistema instável.

2. Anti-Windup

O termo integral acumula o erro. Mas quando o controlador satura a saída, continuar acumulando integral faz o erro “explodir”, produzindo oscilações longas e perda de estabilidade.

Exemplo clássico:

PID pede PWM = 150% → saturação em 100%
Termo integral continua crescendo
Quando o erro muda de sinal, o integral demora a “descarregar”

Para evitar isso, uma solução comum é:

\[
\text{Se } u \text{ saturou, então não atualize o termo integral}
\]

ou uma forma mais suave (back-calculation), que veremos depois.

3. Derivada Filtrada (Filtro Passa-Baixa)

A derivada é extremamente sensível ao ruído. Em motores, fontes chaveadas, sensores barulhentos… o termo D pode oscilar violentamente.

O filtro passa-baixa discreto mais comum é:

\[
D_f[k] = \alpha D_f[k-1] + (1 – \alpha) D_{\text{bruto}}[k]
\]

onde:

\[
\alpha = \frac{\tau_d}{\tau_d + T_s}
\]

e \( \tau_d \) é o tempo do filtro.

Escolhas típicas:

\( \alpha = 0.90 \) (filtro leve)
\( \alpha = 0.98 \) (filtro forte)

4. Estrutura Robusta em C

Agora juntamos tudo: saturação, anti-windup, derivada filtrada.

typedef struct {
    float Kp;
    float Ki;
    float Kd;

    float Ts;                // tempo de amostragem
    float out_min;           // saturação mínima
    float out_max;           // saturação máxima

    // Estado interno
    float integrator; 
    float prev_error;
    float deriv_filtered;
    float alpha;             // coeficiente do filtro derivativo
} PID_Controller;


// Atualiza o PID com anti-windup e D filtrado
float PID_Update(PID_Controller *pid, float setpoint, float measurement) {

    // 1. Erro
    float error = setpoint - measurement;

    // 2. Proporcional
    float P = pid->Kp * error;

    // 3. Integral (somente se NÃO saturado)
    pid->integrator += pid->Ki * pid->Ts * error;

    // 4. Derivada bruta
    float derivative_raw = (error - pid->prev_error) / pid->Ts;

    // 5. Derivada filtrada
    pid->deriv_filtered =
        pid->alpha * pid->deriv_filtered +
        (1.0f - pid->alpha) * derivative_raw;

    float D = pid->Kd * pid->deriv_filtered;

    // 6. Soma
    float output = P + pid->integrator + D;

    // 7. Saturação
    float output_sat = output;
    if (output_sat > pid->out_max) output_sat = pid->out_max;
    else if (output_sat < pid->out_min) output_sat = pid->out_min;

    // 8. Anti-windup (se saturou, desfaz parte da integral)
    if (output != output_sat) {
        // back-calculation clássico
        float aw_gain = 0.5f; // ajustável
        pid->integrator += aw_gain * (output_sat - output);
    }

    // 9. Guarda estado
    pid->prev_error = error;

    return output_sat;
}

typedef struct {
    float Kp;
    float Ki;
    float Kd;

    float Ts;                // tempo de amostragem
    float out_min;           // saturação mínima
    float out_max;           // saturação máxima

    // Estado interno
    float integrator; 
    float prev_error;
    float deriv_filtered;
    float alpha;             // coeficiente do filtro derivativo
} PID_Controller;


// Atualiza o PID com anti-windup e D filtrado
float PID_Update(PID_Controller *pid, float setpoint, float measurement) {

    // 1. Erro
    float error = setpoint - measurement;

    // 2. Proporcional
    float P = pid->Kp * error;

    // 3. Integral (somente se NÃO saturado)
    pid->integrator += pid->Ki * pid->Ts * error;

    // 4. Derivada bruta
    float derivative_raw = (error - pid->prev_error) / pid->Ts;

    // 5. Derivada filtrada
    pid->deriv_filtered =
        pid->alpha * pid->deriv_filtered +
        (1.0f - pid->alpha) * derivative_raw;

    float D = pid->Kd * pid->deriv_filtered;

    // 6. Soma
    float output = P + pid->integrator + D;

    // 7. Saturação
    float output_sat = output;
    if (output_sat > pid->out_max) output_sat = pid->out_max;
    else if (output_sat < pid->out_min) output_sat = pid->out_min;

    // 8. Anti-windup (se saturou, desfaz parte da integral)
    if (output != output_sat) {
        // back-calculation clássico
        float aw_gain = 0.5f; // ajustável
        pid->integrator += aw_gain * (output_sat - output);
    }

    // 9. Guarda estado
    pid->prev_error = error;

    return output_sat;
}

5. Por que esta versão é “industrial”?

Porque inclui todos os elementos necessários para evitar problemas clássicos:

Problemas que esta versão previne:

Saturação violenta do controle
Explosão do termo integral (windup)
Ruído amplificado pelo termo derivativo
Oscilações excessivas em sistemas rápidos
Estouro numérico em microcontroladores de ponto flutuante simples

Onde essa versão é usada?

Controle de velocidade (motores DC ou BLDC)
Controle de temperatura (fornos, resistências, Peltier)
Controle de posição (sistemas robóticos)
Conversores chaveados tipo Buck/Boost
Drones, robôs móveis e estabilizadores

6. Valores típicos de α (filtro derivativo)

Tipo de Sistema	α recomendado	Observações
Sistemas ruidosos (motores DC, sensores Hall)	0.95–0.99	Forte filtragem
Sistemas limpos (encoders ópticos)	0.85–0.95	Mais responsivo
Sistemas de temperatura	0.5–0.7	D quase desnecessário

7. Observação para iniciantes

Nem todo PID precisa de termo D.
Muitas plantas funcionam melhor com PI, especialmente sistemas térmicos.
O termo D deve ser usado com cuidado, e quase sempre com filtro.

Comparação entre PID e Outros Controladores de Malha Fechada

Agora que temos um PID robusto, faz sentido compará-lo com outras estratégias de controle em malha fechada. Isso ajuda a entender quando realmente vale a pena usar PID, quando um PI basta, ou quando um simples on-off resolve o problema.

Vamos comparar:

ON–OFF (tudo ou nada)
P (somente proporcional)
PI (proporcional + integral)
PD (proporcional + derivativo)
PID completo

Sempre com foco em intuição, fórmulas básicas e exemplos em C.

1. Controle ON–OFF (Tudo ou Nada)

É o mais simples de todos. A função de controle é basicamente:

\[
u(t) =
\begin{cases}
u_{\max}, & \text{se } e(t) > \Delta \
u_{\min}, & \text{se } e(t) < -\Delta \
\text{não muda}, & \text{caso contrário}
\end{cases}
\]

onde \( \Delta \) é a histerese.

Características:

Fácil de implementar;
Gera oscilações em torno do setpoint;
Não controla bem tempo de subida, overshoot, etc.;
Bom para sistemas lentos e tolerantes a erro (geladeiras, aquecedores simples, caixas d’água).

Exemplo em C (relembrando, mas simplificado):

float setpoint = 50.0f;
float hysteresis = 1.0f;
int output_on = 0;

float onoff_update(float measurement) {
    float error = setpoint - measurement;

    if (error > hysteresis) {
        output_on = 1;
    } else if (error < -hysteresis) {
        output_on = 0;
    }

    return (float)output_on; // 0 ou 1
}

float setpoint = 50.0f;
float hysteresis = 1.0f;
int output_on = 0;

float onoff_update(float measurement) {
    float error = setpoint - measurement;

    if (error > hysteresis) {
        output_on = 1;
    } else if (error < -hysteresis) {
        output_on = 0;
    }

    return (float)output_on; // 0 ou 1
}

2. Controle Proporcional (P)

Função de controle:

\[
u(t) = K_p \cdot e(t)
\]

No discreto:

\[
u[k] = K_p \cdot e[k]
\]

Características:

Simples;
Resposta mais suave que on–off;
Diminui o erro, mas em geral deixa um erro de regime permanente (offset) quando a planta não é puramente integradora;
Grande \( K_p \) → resposta mais rápida, mas com overshoot e risco de oscilações.

Exemplo em C:

float Kp = 2.0f;

float P_update(float setpoint, float measurement) {
    float error = setpoint - measurement;
    float output = Kp * error;
    return output; // lembrando de saturar em outra função
}

float Kp = 2.0f;

float P_update(float setpoint, float measurement) {
    float error = setpoint - measurement;
    float output = Kp * error;
    return output; // lembrando de saturar em outra função
}

3. Controle Proporcional–Integral (PI)

Função de controle:

\[
u(t) = K_p e(t) + K_i \int_0^t e(\tau) d\tau
\]

No discreto:

\[
\begin{aligned}
u_I[k] &= u_I[k-1] + K_i T_s e[k] \
u[k] &= K_p e[k] + u_I[k]
\end{aligned}
\]

Características:

Elimina o erro de regime permanente;
Muito usado em controle de velocidade e temperatura;
Menos sensível a ruído que PID (sem termo D);
Se o integral for exagerado, causa overshoot grande e oscilações.

Versão simples em C (sem filtros):

typedef struct {
    float Kp;
    float Ki;
    float Ts;
    float integrator;
} PI_Controller;

float PI_Update(PI_Controller *pi, float setpoint, float measurement) {
    float error = setpoint - measurement;

    // Proporcional
    float P = pi->Kp * error;

    // Integral
    pi->integrator += pi->Ki * pi->Ts * error;
    float I = pi->integrator;

    float output = P + I;
    return output;
}

typedef struct {
    float Kp;
    float Ki;
    float Ts;
    float integrator;
} PI_Controller;

float PI_Update(PI_Controller *pi, float setpoint, float measurement) {
    float error = setpoint - measurement;

    // Proporcional
    float P = pi->Kp * error;

    // Integral
    pi->integrator += pi->Ki * pi->Ts * error;
    float I = pi->integrator;

    float output = P + I;
    return output;
}

Na prática, você pode pegar o PID completo da seção anterior e apenas colocar Kd = 0.

4. Controle Proporcional–Derivativo (PD)

Função de controle:

\[
u(t) = K_p e(t) + K_d \frac{de(t)}{dt}
\]

No discreto:

\[
u[k] = K_p e[k] + K_d \frac{e[k] – e[k-1]}{T_s}
\]

Características:

Bom para sistemas onde não precisamos eliminar erro de regime permanente, mas queremos melhorar a resposta transitória (reduzir overshoot, “frear” o sistema);
Pode ser usado como “melhorador de dinâmica” em oposição ao PI, que foca em eliminar erro estacionário;
Muito sensível a ruído se não usar filtro na derivada.

Exemplo em C (usar só para fins didáticos):

typedef struct {
    float Kp;
    float Kd;
    float Ts;
    float prev_error;
} PD_Controller;

float PD_Update(PD_Controller *pd, float setpoint, float measurement) {
    float error = setpoint - measurement;

    // Proporcional
    float P = pd->Kp * error;

    // Derivativo
    float derivative = (error - pd->prev_error) / pd->Ts;
    float D = pd->Kd * derivative;

    pd->prev_error = error;

    float output = P + D;
    return output;
}

typedef struct {
    float Kp;
    float Kd;
    float Ts;
    float prev_error;
} PD_Controller;

float PD_Update(PD_Controller *pd, float setpoint, float measurement) {
    float error = setpoint - measurement;

    // Proporcional
    float P = pd->Kp * error;

    // Derivativo
    float derivative = (error - pd->prev_error) / pd->Ts;
    float D = pd->Kd * derivative;

    pd->prev_error = error;

    float output = P + D;
    return output;
}

5. Controle PID Completo

Função de controle:

\[
u(t) = K_p e(t) + K_i \int_0^t e(\tau), d\tau + K_d \frac{de(t)}{dt}
\]

Em discreto:

\[
u[k] = K_p e[k] + u_I[k] + K_d \frac{e[k] – e[k-1]}{T_s}
\]

Características:

Combina o melhor dos dois mundos:
- P → resposta rápida;
- I → zera erro estacionário;
- D → melhora dinamicamente a resposta (menos overshoot, mais amortecimento);
Exige mais cuidado de sintonia do que P ou PI;
Em muitos sistemas práticos, um bom PI já resolve, e o D é usado apenas em casos específicos (posição, robótica, sistemas muito rápidos).

6. Tabela Comparativa Resumida

Controlador	Erro em regime	Overshoot	Sensibilidade a ruído	Complexidade	Uso típico
ON–OFF	Médio/Alto	Oscila	Baixa	Muito baixa	Temperatura simples, nível
P	Médio	Pode ser alto	Baixa/Media	Baixa	Sistemas simples, controle grosseiro
PI	Baixo (≈0)	Médio	Baixa	Média	Velocidade, temperatura, processos industriais
PD	Médio	Baixo	Alta (sem filtro)	Média	Posição, robótica, sistemas rápidos
PID	Baixo (≈0)	Ajustável	Alta (D precisa de filtro)	Média/Alta	Casos gerais de controle de precisão

7. Quando Escolher Cada Um?

ON–OFF: se o sistema é lento, tolerante a erro e não exige precisão (termostatos simples).
P: quando queremos apenas “melhorar um pouco” a estabilidade e reduzir erro sem necessidade de zerá-lo.
PI: primeira escolha para controle de processos (velocidade, temperatura, nível) onde o erro estacionário deve ser quase zero.
PD: útil em sistemas mecânicos onde já existe alguma integral natural (por exemplo, dinâmica de posição/velocidade) e queremos só “amortecer”.
PID: quando o sistema exige boa dinâmica e erro próximo de zero, e há atenção especial à sintonia e filtragem do derivativo.

Sintonia de PID

(métodos básicos, fórmulas práticas e passo a passo de ajuste com exemplos em C)

A sintonia é o processo de escolher valores adequados para Kp, Ki e Kd. É aqui que o controlador realmente “ganha vida”. Não existe um único método universal, mas há abordagens clássicas, práticas e bem aceitas na engenharia de controle — todas aplicáveis a microcontroladores.

Nesta seção, você aprenderá:

Como cada ganho influencia o comportamento
Métodos clássicos de sintonia (Ziegler–Nichols, método da resposta ao degrau)
Métodos práticos para quem está programando microcontroladores
Exemplos reais em C para ajustes automáticos simples

1. Efeito de Cada Ganho (Intuição Essencial)

Se você entender isso, já terá 50% da sintonia dominada.

1.1 Ganho Proporcional – Kp

Aumenta a velocidade de resposta
Reduz erro transitório
Aumenta overshoot
Pode causar oscilações

Regra prática:
Se o sistema está lento → aumente Kp
Se está oscilando → reduza Kp

1.2 Ganho Integral – Ki

Elimina erro estacionário
Pode causar overshoot
Pode causar oscilações de baixa frequência
É a principal causa de windup

Regra prática:
Se o sistema estabiliza mas não atinge o setpoint → aumente Ki
Se começa a oscilar lentamente → reduza Ki

1.3 Ganho Derivativo – Kd

Melhora o amortecimento
Reduz overshoot
Reduz oscilações
Muito sensível a ruído (use filtro!)

Regra prática:
Se o sistema passa muito do setpoint (overshoot alto) → aumente Kd
Se o sistema responde lentamente, mas sem instabilidade → diminua Kd

2. Métodos de Sintonia

2.1 Ziegler–Nichols Clássico (Método de Oscilação)

Este é o método mais famoso do mundo industrial.

Passos:

Coloque Ki = 0 e Kd = 0
Aumente Kp até o sistema começar a oscilar de forma sustentada
Registre:
- Ku (K ultimate) = ganho que causa oscilação sustentada
- Tu (período da oscilação)

A partir de Ku e Tu aplicam-se fórmulas:

Controlador	Kp	Ki	Kd
P	0.50 Ku	–	–
PI	0.45 Ku	1.2 Kp / Tu	–
PID	0.60 Ku	2 Kp / Tu	Kp Tu / 8

O método é rápido, simples e funciona bem para plantas não muito ruidosas.

2.2 Método da Resposta ao Degrau

Consiste em aplicar um degrau na entrada e medir:

Tempo de subida
Tempo morto
Inclinação inicial

A curva típica é aproximada por um modelo FOPDT:

\[
G(s) = \frac{K}{\tau(1 + sT_d)} e^{-Ls}
\]

Depois aplica-se uma tabela parecida com Ziegler–Nichols.

2.3 Método Manual (prático e recomendado em microcontroladores)

Este método é amplamente usado na prática porque é intuitivo e seguro.

Passo 1 – Ajuste Kp

Comece com Kp baixo
Aumente até que o sistema fique rápido, mas sem oscilar muito

Passo 2 – Ajuste Ki

Aumente Ki até eliminar o erro permanente
Se começar a oscilar lentamente → reduza Ki

Passo 3 – Ajuste Kd

Adicione Kd para reduzir overshoot
Ajuste até encontrar o ponto onde a resposta fica limpa e estável

Este método funciona muito bem mesmo sem conhecimento profundo da planta.

3. Exemplo Prático com Código em C

(Ajuste manual supervisionado por microcontrolador)

Imagine que temos um controlador PID rodando a cada 10 ms controlando velocidade de motor.

Vamos adicionar um ajuste semiautomático, permitindo alterar ganhos via UART ou Bluetooth.

void tune_pid_step(PID_Controller *pid) {
    float error = pid->prev_error;

    // Heurística simples de ajuste
    if (fabs(error) > 10.0f) {
        pid->Kp += 0.01f; // aumentar agressividade
    } else if (fabs(error) < 2.0f) {
        pid->Ki += 0.001f; // remover erro residual
    }

    // Pequeno amortecimento se houver oscilação
    static float sign_prev = 0;
    float sign_now = (error > 0) ? 1 : -1;

    if (sign_now != sign_prev) {
        pid->Kd += 0.005f; // oscila → aumenta termo D
    }

    sign_prev = sign_now;
}

void tune_pid_step(PID_Controller *pid) {
    float error = pid->prev_error;

    // Heurística simples de ajuste
    if (fabs(error) > 10.0f) {
        pid->Kp += 0.01f; // aumentar agressividade
    } else if (fabs(error) < 2.0f) {
        pid->Ki += 0.001f; // remover erro residual
    }

    // Pequeno amortecimento se houver oscilação
    static float sign_prev = 0;
    float sign_now = (error > 0) ? 1 : -1;

    if (sign_now != sign_prev) {
        pid->Kd += 0.005f; // oscila → aumenta termo D
    }

    sign_prev = sign_now;
}

É claro que ajustes automáticos reais são mais sofisticados, mas esse exemplo mostra a ideia.

4. Sintonia Específica para Tipos de Sistemas

4.1 Controle de Temperatura

Use PI
Kp pequeno
Ki pequeno
D quase sempre = 0
Planta muito lenta → filtragem alta

Valores típicos:

Kp = 1.0
Ki = 0.1
Kd = 0.0

Kp = 1.0
Ki = 0.1
Kd = 0.0

4.2 Controle de Velocidade de Motor DC

Use PI ou PID leve
Sistemas moderadamente rápidos
D pode ajudar
Antiwindup obrigatório

Valores típicos:

Kp = 0.3
Ki = 0.05
Kd = 0.01

Kp = 0.3
Ki = 0.05
Kd = 0.01

4.3 Controle de Posição (robótica)

PID completo
D obrigatório
Ki muito baixo

Valores típicos:

Kp = 1.5
Ki = 0.02
Kd = 0.4

Kp = 1.5
Ki = 0.02
Kd = 0.4

5. Armadilhas Comuns

Ki muito alto → instabilidade
Kd sem filtro → ruído amplificado
Kp alto demais → oscilação
Período de amostragem mal escolhido
(ideal: 10–20 vezes mais rápido que a dinâmica da planta)

Exemplos Completos de Aplicação do PID em C

(com Planta Simulada, Controle Realista e Casos Usuais em Engenharia)

Nesta seção vamos consolidar tudo o que estudamos, apresentando exemplos completos, totalmente funcionais e didáticos, em C. Cada exemplo usa:

Planta discreta (simulada ou medida)
PID robusto com anti-windup e filtro derivativo
Código estruturado
Explicação detalhada para iniciantes

Isso permitirá que você implemente em microcontroladores reais (ARM, RISC-V, RP2040, AVR, ESP32 etc.) ou teste diretamente no PC.

1. Exemplo: Controle de Velocidade de Motor DC

(simulação completa com planta discreta)

1.1 Modelo da planta

Motores DC de baixa potência possuem dinâmica aproximada por um sistema de primeira ordem:

\[
y[k] = a \cdot y[k-1] + b \cdot u[k]
\]

Onde:

\( u[k] \) = PWM (0 a 1)
\( y[k] \) = velocidade (RPM normalizada)

1.2 Código completo

#include <stdio.h>
#include <math.h>

typedef struct {
    float Kp, Ki, Kd;
    float Ts;
    float out_min, out_max;

    float integrator;
    float prev_error;
    float deriv_filtered;
    float alpha;
} PID;

float PID_Update(PID *pid, float setpoint, float measurement) {
    float error = setpoint - measurement;

    // Proporcional
    float P = pid->Kp * error;

    // Integral
    pid->integrator += pid->Ki * pid->Ts * error;

    // Derivativa filtrada
    float d_raw = (error - pid->prev_error) / pid->Ts;
    pid->deriv_filtered = pid->alpha * pid->deriv_filtered +
                          (1 - pid->alpha) * d_raw;
    float D = pid->Kd * pid->deriv_filtered;

    // Saída
    float output = P + pid->integrator + D;

    // Saturação
    float out_sat = output;
    if (out_sat > pid->out_max) out_sat = pid->out_max;
    else if (out_sat < pid->out_min) out_sat = pid->out_min;

    // Anti-windup
    if (out_sat != output) {
        pid->integrator += 0.5f * (out_sat - output);
    }

    pid->prev_error = error;
    return out_sat;
}

int main() {
    // Planta de primeira ordem do motor
    float K = 1.0f;      // ganho
    float tau = 0.2f;    // constante de tempo
    float Ts = 0.01f;    // 10 ms
    float a = expf(-Ts / tau);
    float b = K * (1.0f - a);

    PID pid = {
        .Kp = 0.40f, .Ki = 1.0f, .Kd = 0.01f,
        .Ts = Ts,
        .out_min = 0.0f, .out_max = 1.0f,
        .integrator = 0,
        .prev_error = 0,
        .deriv_filtered = 0,
        .alpha = 0.95f
    };

    float y = 0.0f;
    float setpoint = 0.8f; // 80% da velocidade máxima

    for (int k = 0; k < 500; k++) {
        float u = PID_Update(&pid, setpoint, y);   // atualiza controlador
        y = a * y + b * u;                         // atualiza planta
        printf("%d %.4f %.4f\n", k, u, y);
    }
}

#include <stdio.h>
#include <math.h>

typedef struct {
    float Kp, Ki, Kd;
    float Ts;
    float out_min, out_max;

    float integrator;
    float prev_error;
    float deriv_filtered;
    float alpha;
} PID;

float PID_Update(PID *pid, float setpoint, float measurement) {
    float error = setpoint - measurement;

    // Proporcional
    float P = pid->Kp * error;

    // Integral
    pid->integrator += pid->Ki * pid->Ts * error;

    // Derivativa filtrada
    float d_raw = (error - pid->prev_error) / pid->Ts;
    pid->deriv_filtered = pid->alpha * pid->deriv_filtered +
                          (1 - pid->alpha) * d_raw;
    float D = pid->Kd * pid->deriv_filtered;

    // Saída
    float output = P + pid->integrator + D;

    // Saturação
    float out_sat = output;
    if (out_sat > pid->out_max) out_sat = pid->out_max;
    else if (out_sat < pid->out_min) out_sat = pid->out_min;

    // Anti-windup
    if (out_sat != output) {
        pid->integrator += 0.5f * (out_sat - output);
    }

    pid->prev_error = error;
    return out_sat;
}

int main() {
    // Planta de primeira ordem do motor
    float K = 1.0f;      // ganho
    float tau = 0.2f;    // constante de tempo
    float Ts = 0.01f;    // 10 ms
    float a = expf(-Ts / tau);
    float b = K * (1.0f - a);

    PID pid = {
        .Kp = 0.40f, .Ki = 1.0f, .Kd = 0.01f,
        .Ts = Ts,
        .out_min = 0.0f, .out_max = 1.0f,
        .integrator = 0,
        .prev_error = 0,
        .deriv_filtered = 0,
        .alpha = 0.95f
    };

    float y = 0.0f;
    float setpoint = 0.8f; // 80% da velocidade máxima

    for (int k = 0; k < 500; k++) {
        float u = PID_Update(&pid, setpoint, y);   // atualiza controlador
        y = a * y + b * u;                         // atualiza planta
        printf("%d %.4f %.4f\n", k, u, y);
    }
}

1.3 O que observar ao executar:

A velocidade y sobe suavemente até 0.8
Pouco overshoot
Estabilidade garantida
O sinal u (PWM) atinge valores moderados conforme a planta responde

Esse é o mesmo mecanismo usado em controle de velocidade de motores em robôs, ventiladores, atuadores lineares etc.

2. Exemplo: Controle de Temperatura (PI)

Plantas térmicas são lentas e geralmente não precisam do termo derivativo.

2.1 Modelo térmico simples

\[
T[k] = a T[k-1] + b u[k]
\]

Com:

a ≈ 0.99 para sistemas muito lentos
u[k] = potência (0–1)

2.2 Código PI reduzido

typedef struct {
    float Kp, Ki;
    float Ts;
    float integrator;
    float out_min, out_max;
} PI;

float PI_Update(PI *pi, float setpoint, float T) {
    float error = setpoint - T;

    float P = pi->Kp * error;
    pi->integrator += pi->Ki * pi->Ts * error;

    float out = P + pi->integrator;

    if (out > pi->out_max) {
        out = pi->out_max;
        pi->integrator -= pi->Ki * pi->Ts * error;
    }
    else if (out < pi->out_min) {
        out = pi->out_min;
        pi->integrator -= pi->Ki * pi->Ts * error;
    }

    return out;
}

typedef struct {
    float Kp, Ki;
    float Ts;
    float integrator;
    float out_min, out_max;
} PI;

float PI_Update(PI *pi, float setpoint, float T) {
    float error = setpoint - T;

    float P = pi->Kp * error;
    pi->integrator += pi->Ki * pi->Ts * error;

    float out = P + pi->integrator;

    if (out > pi->out_max) {
        out = pi->out_max;
        pi->integrator -= pi->Ki * pi->Ts * error;
    }
    else if (out < pi->out_min) {
        out = pi->out_min;
        pi->integrator -= pi->Ki * pi->Ts * error;
    }

    return out;
}

Este código é praticamente o usado em aquecedores, estufas, controle de hotend de impressoras 3D, reatores químicos pequenos etc.

3. Exemplo: Controle de Posição (PID com D forte)

Plantas de posição normalmente se comportam como integração dupla (velocidade + posição), exigindo:

Kp alto
Ki baixo (para evitar drift)
Kd alto (para amortecer)

3.1 Código de aplicação

float position_controller(PID *pid, float desired_position, float measured_position) {
    return PID_Update(pid, desired_position, measured_position);
}

float position_controller(PID *pid, float desired_position, float measured_position) {
    return PID_Update(pid, desired_position, measured_position);
}

Esse controlador é adequado para:

Controle de eixos robóticos
Máquinas CNC pequenas
Gimbals e estabilizadores

4. Exemplo: Simulador Completo em C

(para teste de diferentes controladores)

O código abaixo permite trocar entre P, PI e PID facilmente para comparar respostas:

typedef enum { CTL_P, CTL_PI, CTL_PID } control_mode_t;

float control_step(control_mode_t mode,
                   PID *pid, PI *pi,
                   float setpoint, float y) 
{
    switch (mode) {
        case CTL_P:
            return pid->Kp * (setpoint - y);

        case CTL_PI:
            return PI_Update(pi, setpoint, y);

        case CTL_PID:
        default:
            return PID_Update(pid, setpoint, y);
    }
}

typedef enum { CTL_P, CTL_PI, CTL_PID } control_mode_t;

float control_step(control_mode_t mode,
                   PID *pid, PI *pi,
                   float setpoint, float y) 
{
    switch (mode) {
        case CTL_P:
            return pid->Kp * (setpoint - y);

        case CTL_PI:
            return PI_Update(pi, setpoint, y);

        case CTL_PID:
        default:
            return PID_Update(pid, setpoint, y);
    }
}

Assim é possível comparar dinamicamente:

Overshoot
Tempo de subida
Erro estacionário
Estabilidade

5. Lições Práticas desta Seção

Simular plantas ajuda demais na compreensão do PID.
PID completo é mais útil em sistemas rápidos e mecânicos (motores, robótica).
PI é excelente para sistemas térmicos e processos lentos.
Saturação e anti-windup são essenciais em qualquer microcontrolador.
Derivada filtrada é obrigatória em aplicações reais com ruído.

Conclusão Geral

O controlador PID permanece como o padrão-ouro em engenharia de controle porque equilibra simplicidade, robustez e capacidade de ajuste fino para diversos tipos de plantas. Ele é suficientemente poderoso para controlar motores, temperatura, posição, tensão, corrente e sistemas mecânicos complexos, mas ao mesmo tempo simples o bastante para ser implementado em C em microcontroladores com recursos limitados.

O uso eficiente do PID exige três pilares fundamentais:

Modelagem mínima da planta — mesmo aproximações simples (primeira ordem) já permitem prever comportamento e ajustar expectativas.
Sintonia adequada dos ganhos — métodos manuais, Ziegler–Nichols ou heurísticos específicos do tipo de sistema permitem ajustar o equilíbrio entre agressividade e estabilidade.
Implementação robusta — indispensável em aplicações reais: saturação, anti-windup e filtragem derivativa evitam problemas comuns como oscilações, ruído amplificado e demora para recuperar o controle.

Controladores mais simples como P, PI e ON–OFF têm seu valor: em sistemas lentos, ruidosos ou economicamente restritos, são frequentemente suficientes. Já aplicações mais exigentes, como robótica, veículos autônomos, power electronics e sistemas de alta precisão, beneficiam-se do PID completo com técnicas adicionais de estabilização.

O conhecimento apresentado aqui é suficiente para que você:

Implemente com segurança um PID em qualquer microcontrolador
Simule a planta e prever a resposta
Compare e escolher o tipo de controlador adequado
Ajuste o comportamento do sistema conforme requisitos reais

Com isso, você está pronto para aplicar controle PID com confiança em projetos profissionais, acadêmicos e industriais.

PID na Prática: Fundamentos, Fórmulas, Simulação e Implementação em C para Sistemas Embarcados

O que é o PID em termos intuitivos?

Por que o PID é tão usado?

Controle em malha fechada simples x PID

Visão geral do que virá nas próximas seções

Modelagem Simples da Planta e Comportamento de Malha Fechada

1. O que é uma Planta em Controle?

2. Exemplo Didático: Planta de Primeira Ordem

3. Solução do Modelo — Resposta ao Degrau

4. Planta Discreta (para implementação em C)

5. Exemplo em C — Simulação de uma Planta de Primeira Ordem

6. O que Você Deve Perceber Dessa Seção

Derivação Completa do Controlador PID (Contínuo e Discreto)

1. Revisão Intuitiva das Três Ações

2. Forma Contínua do PID

3. Discretização do PID (Amostragem)

3.1 Erro discreto

4. Ação Proporcional (discreta)

5. Ação Integral (discreta)

6. Ação Derivativa (discreta)

7. Fórmula Completa do PID Discreto

8. Implementação do PID Discreto — Versão Didática em C

9. O que você deve entender desta seção

Implementação Completa do PID em C

1. Saturação da Saída (Clamping)

2. Anti-Windup

3. Derivada Filtrada (Filtro Passa-Baixa)

4. Estrutura Robusta em C

5. Por que esta versão é “industrial”?

Problemas que esta versão previne:

Onde essa versão é usada?

6. Valores típicos de α (filtro derivativo)

7. Observação para iniciantes

Comparação entre PID e Outros Controladores de Malha Fechada

1. Controle ON–OFF (Tudo ou Nada)

2. Controle Proporcional (P)

3. Controle Proporcional–Integral (PI)

4. Controle Proporcional–Derivativo (PD)

5. Controle PID Completo

6. Tabela Comparativa Resumida

7. Quando Escolher Cada Um?

Sintonia de PID

1. Efeito de Cada Ganho (Intuição Essencial)

1.1 Ganho Proporcional – Kp

1.2 Ganho Integral – Ki

1.3 Ganho Derivativo – Kd

2. Métodos de Sintonia

2.1 Ziegler–Nichols Clássico (Método de Oscilação)

Passos:

2.2 Método da Resposta ao Degrau

2.3 Método Manual (prático e recomendado em microcontroladores)

Passo 1 – Ajuste Kp

Passo 2 – Ajuste Ki

Passo 3 – Ajuste Kd

3. Exemplo Prático com Código em C

4. Sintonia Específica para Tipos de Sistemas

4.1 Controle de Temperatura

4.2 Controle de Velocidade de Motor DC

4.3 Controle de Posição (robótica)

5. Armadilhas Comuns

Exemplos Completos de Aplicação do PID em C

1. Exemplo: Controle de Velocidade de Motor DC

1.1 Modelo da planta

1.2 Código completo

1.3 O que observar ao executar:

2. Exemplo: Controle de Temperatura (PI)

2.1 Modelo térmico simples

2.2 Código PI reduzido

3. Exemplo: Controle de Posição (PID com D forte)

3.1 Código de aplicação

4. Exemplo: Simulador Completo em C

5. Lições Práticas desta Seção

Conclusão Geral

Related Post

Algoritmos de Controle de Loop Fechado: Guia Completo com PID e Exemplos em CAlgoritmos de Controle de Loop Fechado: Guia Completo com PID e Exemplos em C

Como Firmwares Conscientes de Energia Podem Prevenir Falhas de HardwareComo Firmwares Conscientes de Energia Podem Prevenir Falhas de Hardware

Introdução ao Radar FMCWIntrodução ao Radar FMCW