Ângulos de Euler
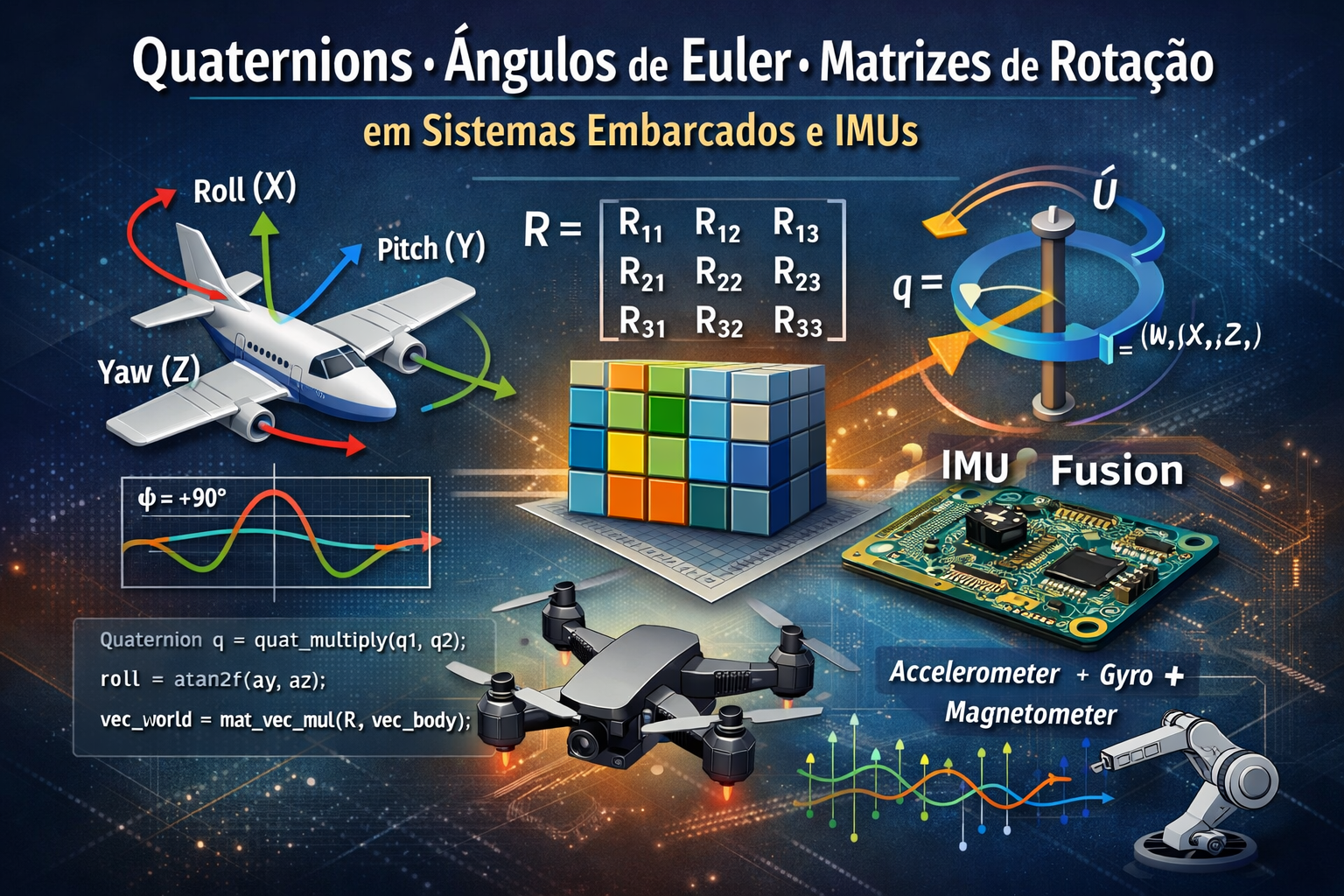
Ângulos de Euler são provavelmente a forma mais intuitiva de representar orientação. Eles descrevem a rotação de um corpo rígido no espaço a partir de três rotações sucessivas em torno de eixos coordenados. Em sistemas embarcados, especialmente em aplicações com IMU, é comum usar a convenção roll, pitch e yaw. O roll é a rotação em torno do eixo X do corpo, o pitch em torno do eixo Y e o yaw em torno do eixo Z. Em um drone, por exemplo, roll representa a inclinação lateral, pitch a inclinação para frente ou para trás, e yaw a rotação horizontal como se fosse uma bússola.
Matematicamente, os ângulos de Euler são aplicados de forma sequencial. Isso é fundamental: a ordem importa. Uma rotação em X seguida de Y não é igual a Y seguida de X. Uma convenção muito usada é Z-Y-X, isto é, primeiro yaw (Z), depois pitch (Y), depois roll (X). Essa composição pode ser representada por uma matriz de rotação resultante, obtida multiplicando as matrizes elementares de cada eixo. Essa matriz transforma vetores do referencial do corpo para o referencial do mundo, ou vice-versa, dependendo da convenção adotada.
Se considerarmos a convenção Z-Y-X, a matriz de rotação R pode ser escrita como:
R = Rz(yaw) * Ry(pitch) * Rx(roll)
Onde cada matriz elementar é:
Rx(roll):
[ 1 0 0 ][ 0 cos(r) -sin(r) ]
[ 0 sin(r) cos(r) ]
Ry(pitch):
[ cos(p) 0 sin(p) ][ 0 1 0 ]
[ -sin(p) 0 cos(p) ]
Rz(yaw):
[ cos(y) -sin(y) 0 ][ sin(y) cos(y) 0 ]
[ 0 0 1 ]
Esse formalismo permite, por exemplo, pegar um vetor medido no referencial do sensor (como a gravidade no acelerômetro) e transformá-lo para o referencial global.
Do ponto de vista prático em firmware, é comum calcular roll e pitch diretamente do acelerômetro quando o sistema está parado, usando trigonometria. Se assumirmos que o acelerômetro mede apenas gravidade (sem aceleração linear), podemos estimar:
roll = atan2(ay, az)
pitch = atan2(-ax, sqrt(ay² + az²))
O yaw não pode ser obtido apenas com acelerômetro; ele depende de magnetômetro ou integração do giroscópio.
Abaixo um exemplo em C demonstrando como calcular roll e pitch a partir de leituras de acelerômetro:
#include <math.h>
#include <stdio.h>
/**
* Estrutura para armazenar ângulos de Euler em radianos.
*/
typedef struct
{
float roll; // Rotação em torno do eixo X
float pitch; // Rotação em torno do eixo Y
float yaw; // Rotação em torno do eixo Z
} EulerAngles;
/**
* @brief Calcula roll e pitch a partir do acelerômetro.
*
* @param ax Aceleração no eixo X (em g ou m/s²)
* @param ay Aceleração no eixo Y
* @param az Aceleração no eixo Z
* @return EulerAngles Estrutura contendo roll e pitch estimados
*/
EulerAngles euler_from_accel(float ax, float ay, float az)
{
EulerAngles angles;
// Roll: rotação em torno de X
angles.roll = atan2f(ay, az);
// Pitch: rotação em torno de Y
angles.pitch = atan2f(-ax, sqrtf(ay * ay + az * az));
// Yaw não pode ser determinado apenas com acelerômetro
angles.yaw = 0.0f;
return angles;
}
int main(void)
{
// Exemplo de leitura simulada do acelerômetro
float ax = 0.0f;
float ay = 0.5f;
float az = 0.866f; // Aproximadamente cos(30°)
EulerAngles angles = euler_from_accel(ax, ay, az);
printf("Roll (rad): %f\n", angles.roll);
printf("Pitch (rad): %f\n", angles.pitch);
return 0;
}
Observe que estamos assumindo um sistema estático. Em movimento real, a aceleração linear contamina a estimativa, e por isso usamos filtros de fusão sensorial (como complementar, Mahony ou Madgwick) para combinar acelerômetro e giroscópio.
O grande problema dos ângulos de Euler é o gimbal lock. Ele ocorre quando pitch atinge ±90°, fazendo com que os eixos de roll e yaw se alinhem, resultando em perda de um grau de liberdade. Matematicamente, isso significa que diferentes combinações de ângulos passam a representar a mesma orientação. Em aplicações como robótica, drones ou controle de atitude, isso é inaceitável, pois você perde estabilidade e continuidade na representação.
Mesmo com essas limitações, ângulos de Euler continuam extremamente úteis para visualização, configuração de limites de controle e interpretação humana da orientação.