MCU.TEC Algoritimos Subtractive Dither na Minimização de Ruídos de Quantização em Conversores ADC e DAC

Subtractive Dither na Minimização de Ruídos de Quantização em Conversores ADC e DAC

07/09/202507/09/2025| Carlos DelfinoCarlos Delfino| 0 Comments | 19:48
Categories:

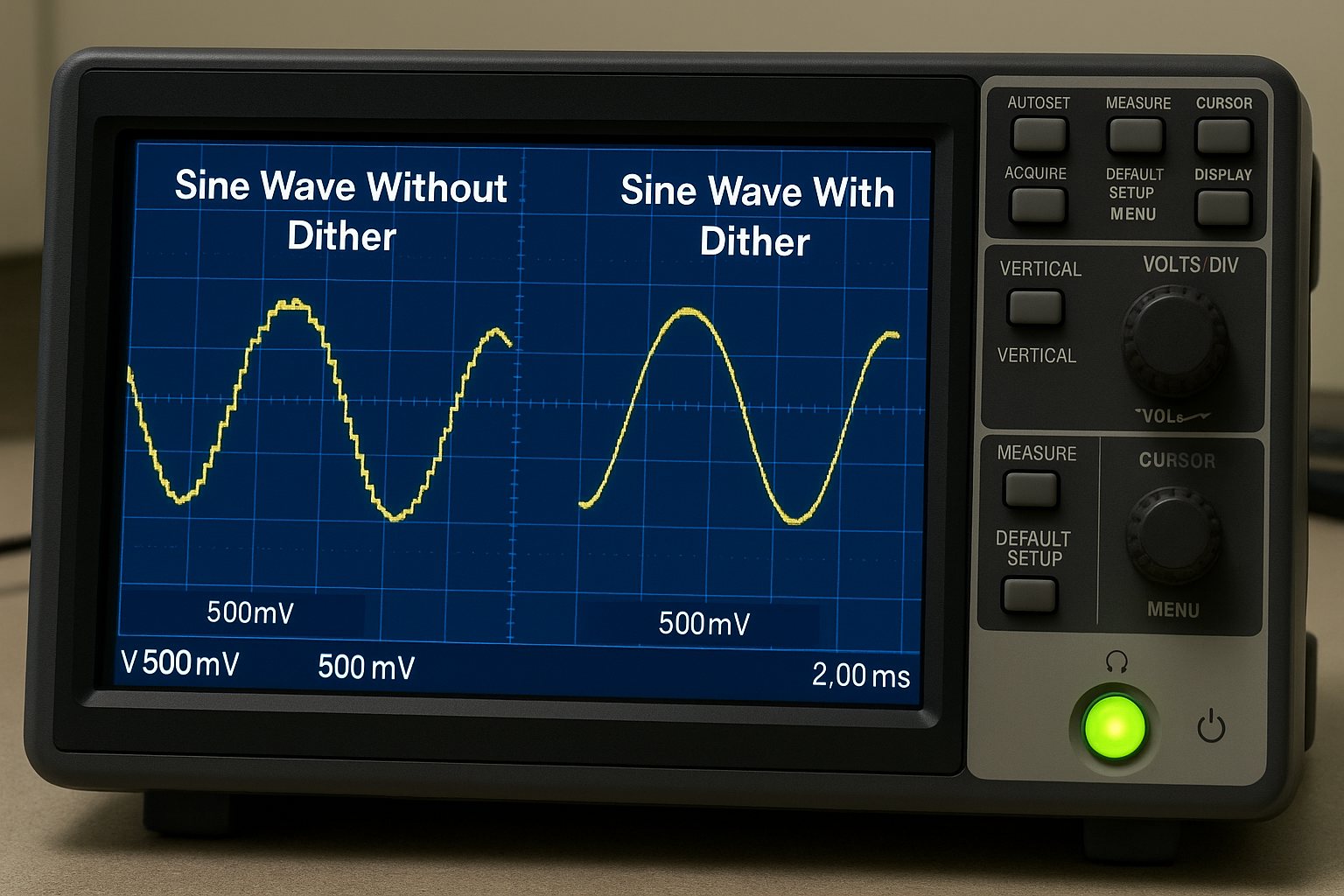
Em sistemas digitais de processamento de sinais, a conversão entre os domínios analógico e digital é inevitável. Conversores analógico-digital (ADC – Analog-to-Digital Converter) e digital-analógico (DAC – Digital-to-Analog Converter) são responsáveis por transformar sinais contínuos em representações discretas e vice-versa. No entanto, esse processo introduz um fenômeno intrínseco: o ruído de quantização. Esse ruído surge da limitação de resolução do conversor, já que um número infinito de valores analógicos é mapeado para um conjunto finito de níveis digitais. O erro entre o valor real e o quantizado se manifesta como distorção ou ruído, especialmente perceptível em sinais de baixa amplitude ou em aplicações de áudio e instrumentação de alta precisão.

Para mitigar esses efeitos, técnicas de dithering são empregadas. O termo dither refere-se à adição de um sinal de baixa amplitude, tipicamente ruído branco, antes do processo de quantização. Essa perturbação, embora contraintuitiva, distribui de forma mais uniforme os erros de quantização, reduzindo sua correlação com o sinal original. Assim, o ruído introduzido se aproxima de um ruído branco não correlacionado, mais fácil de tratar ou mascarar perceptualmente.

Entre as diferentes abordagens, o subtractive dither se destaca por sua eficiência. Nesse método, o ruído adicionado antes da quantização é posteriormente subtraído após a reconstrução do sinal, de modo que a energia espectral do dither não permaneça no resultado final. Isso permite obter os benefícios do dithering (decorrelação do erro de quantização) sem comprometer a relação sinal-ruído (SNR) global do sistema. Essa técnica é amplamente utilizada em sistemas de áudio digital, instrumentação científica e aplicações de controle em que a fidelidade do sinal é crítica.

Fundamentação Teórica

O processo de quantização pode ser modelado matematicamente como a soma do sinal original com um erro de quantização. Sejam:

  • \(x(t)\) → sinal analógico de entrada.
  • \(Q\{\cdot\}\) → operador de quantização.
  • Δ → passo de quantização (intervalo entre dois níveis discretos).

A saída do quantizador pode ser descrita como: \[x_q(t) = Q\{x(t)\} = x(t) + e_q(t)\]

onde o erro de quantização eq(t)e_q(t) é limitado ao intervalo: \[-\frac{\Delta}{2} \leq e_q(t) \leq \frac{\Delta}{2}\]

Se nenhum dither for aplicado, esse erro depende fortemente da entrada, resultando em distorção harmônica correlacionada ao sinal.

Conceito de Dither

Para reduzir essa correlação, adiciona-se um sinal aleatório d(t)d(t), conhecido como dither, antes da quantização: \[x_d(t) = x(t) + d(t)\]

Após a quantização: \[x_{qd}(t) = Q\{x_d(t)\} = x(t) + d(t) + e_q(t)\]

Se o dither for bem projetado (por exemplo, ruído branco uniforme entre \(-\frac{\Delta}{2}\) e \(+\frac{\Delta}{2})\), o erro de quantização \(e_q(t)\) torna-se estatisticamente independente do sinal de entrada. Isso transforma a distorção em um ruído branco aditivo, cuja variância é: \[\sigma_{e_q}^2 = \frac{\Delta^2}{12}\]

Subtractive Dither

No método de subtractive dither, o mesmo sinal de dither \(d(t)\) é conhecido no receptor e subtraído após a quantização: \[x_{out}(t) = x_{qd}(t) – d(t) = x(t) + e_q(t)\]

Note que, apesar de o dither ter sido retirado, sua presença durante a quantização foi suficiente para decorrelacionar o erro de quantização do sinal. O resultado é que \(e_q(t)\) permanece estatisticamente branco, mas sem o acréscimo permanente de ruído do dither no canal de saída. Assim, obtém-se a vantagem de mascaramento das distorções sem degradar a SNR final.

Em resumo, o subtractive dither transforma o erro de quantização em ruído branco não correlacionado, mantendo a energia espectral do sinal livre do ruído artificial que foi temporariamente introduzido.

Exemplo Prático com Fórmulas

Para ilustrar o efeito do subtractive dither, consideremos um sinal senoidal de baixa frequência: \[x(t) = A \cdot \sin(2 \pi f t)\]

com \(A = 0,8 V\) e \(f = 1 \, \text{kHz}\).
Suponhamos que este sinal seja quantizado por um ADC de 3 bits com faixa de entrada de \([-1, \, 1] V\).

Sem Dither

O passo de quantização é: \[\Delta = \frac{2}{2^3} = 0,25 \, \text{V}\]

O erro de quantização máximo é: \[e_q(t) \in \left[-\frac{\Delta}{2}, \, \frac{\Delta}{2}\right] = [-0,125, \, +0,125] \, \text{V}\]

Sem dither, esse erro não é aleatório: ele gera distorções harmônicas, pois os degraus do ADC repetem-se de forma sistemática em relação ao sinal.

Com Dither Aditivo

Se adicionarmos um dither uniforme \(d(t) \sim U(-\frac{\Delta}{2}, +\frac{\Delta}{2})\), temos: \(x_d(t) = x(t) + d(t)\)

Após a quantização: \(x_{qd}(t) = Q\{x_d(t)\} = x(t) + d(t) + e_q(t)\)

Neste caso, o erro de quantização eq(t)e_q(t) torna-se estatisticamente independente de \(x(t)\). O espectro resultante mostra que as harmônicas desaparecem e são substituídas por ruído de fundo.

Com Subtractive Dither

Agora, no receptor (ou pós-processamento), subtraímos o mesmo \(x_{out}(t) = x_{qd}(t) – d(t) = x(t) + e_q(t)\)

Observe que o ruído d(t) não aparece na saída. O erro \(e_q(t)\), porém, já foi descorrelacionado do sinal devido à presença de d(t)d(t) durante a quantização. Assim, o espectro final mostra o sinal senoidal puro, com um ruído branco de potência constante, mas sem distorções harmônicas.

Exemplo Numérico

Para \(A = 0,8 \, \text{V}\) e \(f = 1 \, \text{kHz}:\)

  • Sem dither: o espectro do sinal quantizado apresenta harmônicos em \(2f, 3f, 4f, \dots\).
  • Com subtractive dither: os harmônicos desaparecem, e o ruído é distribuído uniformemente no espectro até a frequência de Nyquist \((f_s/2)\).

A variância do ruído de quantização permanece: \(\sigma_{e_q}^2 = \frac{\Delta^2}{12} = \frac{0,25^2}{12} \approx 0,0052 \, \text{V}^2\)

mas sua percepção é reduzida porque não há distorção tonal correlacionada ao sinal.

Implementação em Hardware Real (RP2040 + BitDogLab)

Abaixo está um exemplo didático em C (Pico SDK) que:

  1. amostra o microfone via ADC do RP2040;
  2. simula a requantização para menos bits (um “ADC virtual” de NN bits) de duas formas: sem dither e com subtractive dither;
  3. calcula a correlação entre o erro de quantização e o sinal para comparar os casos;
  4. exibe no OLED SSD1306 (I²C) as métricas principais (correlação e RMS do erro).

Observações importantes (para manter fidelidade e não “inventar”):
• O BitDogLab usa um microfone conectado a um canal ADC do RP2040 (confira o esquemático específico da sua placa; em muitos kits educacionais o mic vai ao ADC0 no GPIO26). Ajuste ADC_INPUT se necessário. O RP2040 tem ADC de 12 bits com amostragem por hardware_adc do Pico SDK. (datasheets.raspberrypi.com, raspberrypi.com)
• O SSD1306 é um OLED 128×64; abaixo segue uma inicialização mínima por I²C (ajuste endereço 0x3C/0x3D conforme o seu módulo). O controlador, mapeamento de GDDRAM e comandos básicos constam no datasheet oficial. (cdn-shop.adafruit.com, solomon-systech.com, radiolocman.com)

Ideia do pipeline (didático)

  • Capturar um bloco de MM amostras x[n]x[n] do ADC (12 bits nativo).
  • Normalizar para [-1,1].
  • Requantizar digitalmente para NN bits com passo \(\Delta = 2/2^N\):
    • Sem dither: \(y_0[n] = Q\{x[n]\}\).
    • Subtractive dither: gerar \(\sim U(-\Delta/2,\Delta/2)\), aplicar \(y_1[n] = Q\{x[n]+d[n]\} – d[n]\).
  • Estimar correlação \(\rho_{e,x}\) entre erro e[n]=y[n]-x[n] e o sinal x[n] (quanto menor ∣ρ∣|\rho|, melhor a descorrelação).
  • Mostrar ρ e \( \mathrm{rms}(e)\) para os dois casos no OLED.

Código C (Pico SDK + I²C SSD1306, compacto e comentado)

// Subtractive Dither demo for RP2040 + BitDogLab (OLED SSD1306)
// Toolchain: Pico SDK
// Files: CMakeLists.txt deve linkar pico_stdlib, hardware_adc, hardware_i2c
// Atenção: ajuste pinos (I2C, ADC) e endereço do OLED conforme seu hardware.
// ---------------- Includes & Config ----------------
#include <math.h>
#include <stdio.h>
#include <string.h>
#include "pico/stdlib.h"
#include "hardware/adc.h"
#include "hardware/i2c.h"

// ==== Ajustes de hardware (confirme no seu BitDogLab!) ====
#define I2C_PORT       i2c0
#define I2C_SDA_PIN    4    
// ajuste se necessário
#define I2C_SCL_PIN    5     
// ajuste se necessário
#define SSD1306_ADDR   0x3C  // 0x3C ou 0x3D
#define ADC_INPUT      0     // ADC0 (GPIO26) por padrão; altere se preciso
#define ADC_PIN        26    // GPIO26 para ADC0
#define VREF           3.3f  // referência típica RP2040 (use valor medido se quiser mais precisão)
#define FS_HZ          16000 // taxa de amostragem didática (aprox., via sleep)
#define BLOCK_SIZE     512   // tamanho do bloco para métricas
#define NBITS_VIRT     8     // "ADC virtual" de N bits para re-quantização didática
// ---------------- Utilitários matemáticos ----------------
static inline float clampf(float x, float a, float b) { return x < a ? a : (x > b ? b : x); }
// Quantizador uniforme simétrico em [-1,1] com N bits (passo Δ = 2/2^N)
static inline float quantize_uniform(float x, int nbits) {
    const float levels = (float)(1u << nbits);       // 2^N
    const float qstep  = 2.0f / levels;              // Δ
    // map [-1,1] -> índices [0..levels-1]
    float idx = floorf((x + 1.0f) / qstep + 0.5f);   // arredonda ao nível mais próximo
    idx = clampf(idx, 0.0f, levels - 1.0f);<br>    // volta ao valor quantizado no centro do nível
    float y = (idx + 0.5f) * qstep - 1.0f;
    return y;
}
// PRNG simples (Xorshift32) – apenas para gerar dither reprodutível
static uint32_t rng_state = 0x12345678u;
static inline uint32_t xorshift32(void){
    uint32_t x = rng_state;
    x ^= x << 13; x ^= x >> 17; x ^= x << 5;
    return rng_state = x;
}
// Dither U(-Δ/2, +Δ/2)
static inline float dither_uniform(float qstep) {
    // uniforme em [0,1): (xorshift32 & 0xFFFFFF)/2^24
    float u = (float)(xorshift32() & 0xFFFFFFu) / (float)(1<<24);
    return (u - 0.5f) * qstep;
}
// Correlação de Pearson entre e[n] e x[n]
static void corr_and_rms(const float *x, const float *y, int N, float *rho, float *rms_e){
    double sx=0, sy=0, sxx=0, syy=0, sxy=0;
    for(int i=0;i<N;i++){
        const double xi = x[i];
        const double ei = (double)(y[i] - x[i]);
        sx  += xi;  sy  += ei;
        sxx += xi*xi; syy += ei*ei;
        sxy += xi*ei;
    }
    const double Nx = (double)N;
    const double num = sxy - (sx*sy)/Nx;
    const double den = sqrt((sxx - sx*sx/Nx)*(syy - sy*sy/Nx));
    *rho   = (den > 0) ? (float)(num/den) : 0.0f;
    *rms_e = (float)sqrt(syy/Nx);<br>}<br>
// ---------------- Main ----------------
int main() {
    stdio_init_all();
    // I2C
    i2c_init(I2C_PORT, 400*1000);
    gpio_set_function(I2C_SDA_PIN, GPIO_FUNC_I2C);
    gpio_set_function(I2C_SCL_PIN, GPIO_FUNC_I2C);
    gpio_pull_up(I2C_SDA_PIN);
    gpio_pull_up(I2C_SCL_PIN);
    ssd1306_init();
    ssd1306_clear();
    // ADC
    adc_init();
    adc_gpio_init(ADC_PIN);
    adc_select_input(ADC_INPUT);
    // Buffers
    static float x[BLOCK_SIZE];
    // sinal normalizado [-1,1]
    static float y0[BLOCK_SIZE];    // sem dither
    static float y1[BLOCK_SIZE];    // subtractive dither
    const float levels = (float)(1u << NBITS_VIRT);
    const float qstep  = 2.0f / levels; // Δ
    char line[64];
    while (true) {
        // 1) Aquisição (amostra aproximada em FS_HZ via sleep; para FS exato use PIO/DMA)
        for (int n = 0; n < BLOCK_SIZE; n++) {
            uint16_t raw = adc_read(); // 12 bits úteis (0..4095)
            float v = (float)raw * (VREF/4095.0f);     // 0..Vref
            float xn = (v / VREF) * 2.0f - 1.0f;       // normaliza p/ [-1,1]
            x[n] = clampf(xn, -1.0f, 1.0f);
            sleep_us(1000000/FS_HZ);
        }
        // 2) Re-quantização didática (N bits)
        // 2a) Sem dither
        for (int n=0;n<BLOCK_SIZE;n++)
            y0[n] = quantize_uniform(x[n], NBITS_VIRT);
        // 2b) Subtractive dither: y = Q(x + d) - d, com d ~ U(-Δ/2, +Δ/2)
        //    (o mesmo PRNG gera d tanto antes quanto "depois" – aqui, tudo local)
        uint32_t save_state = rng_state; // grava semente para "subtrair" o mesmo d
        for (int n=0;n<BLOCK_SIZE;n++) {
            float d = dither_uniform(qstep);
            y1[n] = quantize_uniform(x[n] + d, NBITS_VIRT);<br>        }
        rng_state = save_state; // ressincroniza para gerar o MESMO d
        for (int n=0;n<BLOCK_SIZE;n++) {
            float d = dither_uniform(qstep);
            y1[n] -= d; // subtractive: remove o dither
        }
        // 3) Métricas
        float rho0, rms0, rho1, rms1;
        corr_and_rms(x, y0, BLOCK_SIZE, &rho0, &rms0);
        corr_and_rms(x, y1, BLOCK_SIZE, &rho1, &rms1);
        // 4) Display no OLED
        ssd1306_clear();
        snprintf(line, sizeof(line), "Nbits=%d FS=%dHz", NBITS_VIRT, FS_HZ);
        ssd1306_print(0, 0, line);
        ssd1306_print(0, 2, "Sem dither:");
        snprintf(line, sizeof(line), "rho=%.3f  rms=%.4f", rho0, rms0);
        ssd1306_print(0, 3, line);
        ssd1306_print(0, 5, "Subtractive:");
        snprintf(line, sizeof(line), "rho=%.3f  rms=%.4f", rho1, rms1);
        ssd1306_print(0, 6, line);
        // Pequena pausa entre blocos
        sleep_ms(80);
    }
    return 0;
  }

Por que esta implementação respeita a teoria?

  • No subtractive dither ideal, o ruído adicionado antes do quantizador é conhecido e subtraído depois. Assim, o erro de quantização resultante torna-se (aprox.) branco e descorrelacionado do sinal, sem carregar o ruído do dither para a saída final. O modelo e as condições para independência/“branqueamento” do erro são bem estabelecidos na literatura clássica (Widrow; Lipshitz, Vanderkooy & Wannamaker; Gray & Stockham). (isl.stanford.edu, convexoptimization.com, ACM Digital Library)

Nota prática para ADCs reais: Em hardware, aplicar subtractive dither “puro” num ADC requer injetar dither analógico bem-definido antes da conversão e conhecer o mesmo dither no processamento (p.ex., ruído pseudo-aleatório gerado por uma fonte sincronizada). No demo acima, simulamos a requantização para N bits após a aquisição de 12 bits — isso permite demonstrar com fidelidade conceitual a diferença entre “sem dither” e “subtractive dither”, inclusive a métrica de correlação \(\rho_{e,x}\). A teoria que justifica a redução de distorção e a “brancura” do erro está nas referências. (convexoptimization.com, isl.stanford.edu)

Resultados

O que você deverá observar no OLED:

  • Sem dither: a correlação \(|\rho_{e,x}|\) tende a ser maior (o erro “segue” o sinal), e o espectro (se você inspecionar numa ferramenta externa) mostra linhas harmônicas — o típico “ruído/distorção de degrau”.
  • Com subtractive dither: \(|\rho_{e,x}|\) cai próximo de zero (erro pouco correlacionado) e o ruído aparece mais branco (energia espalhada), sem as harmônicas proeminentes. A RMS do erro permanece próxima a \(\Delta/\sqrt{12}\) para quantização uniforme, preservando a análise clássica (o ganho está em trocar distorção correlacionada por ruído branco). (isl.stanford.edu)

Por que isso importa em prática (áudio/instrumentação):

  • Distorção harmônica correlacionada é perceptualmente pior (tons parasitas). O dither “troca” isso por ruído estacionário de pequena potência, perceptualmente menos intrusivo; no modelo subtrativo, não “carregamos” o dither para a saída final, mantendo SNR e linearidade efetiva melhores em baixos níveis de sinal. Esses pontos são consolidados na literatura AES e no corpo clássico de dither. (convexoptimization.com, sjeng.org)

Conclusão

O subtractive dither é um recurso essencial para converter erro de quantização estrutural e correlacionado em ruído branco aditivo praticamente independente do sinal, sem penalizar a saída com a energia do dither. Em ADCs e DACs, isso se traduz em menor distorção audível, melhor linearidade aparente em baixos níveis e respostas espectrais mais limpas. No RP2040, a demonstração por requantização virtual reproduz os efeitos fundamentais com simplicidade, permitindo medir diretamente a descorrelação \(\rho_{e,x}\) e a RMS do erro — evidências claras do benefício do método. (convexoptimization.com, isl.stanford.edu)

Referências (fontes reais)

  • Lipshitz, S. P.; Wannamaker, R. A.; Vanderkooy, J. “Quantization and Dither: A Theoretical Survey.” Journal of the Audio Engineering Society, survey clássico cobrindo quantização sem, com dither não-subtrativo e subtrativo, com condições formais para “branqueamento” do erro. (convexoptimization.com)
  • Widrow, B.; Kollar, I. “Statistical Theory of Quantization.” Revisita e estende a teoria estatística de Widrow: quando e por que o ruído de quantização pode ser modelado como branco e independente; base para os modelos com dither. (isl.stanford.edu, pp.bme.hu)
  • Gray, R. M.; Stockham, T. G. “Dithered Quantizers.” IEEE Transactions on Information Theory, 1993. Lança fundamentos de dither no arcabouço de teoria da informação para quantizadores. (ACM Digital Library)
  • Wannamaker, R. A. “The Theory of Dithered Quantization.” Tese e trabalhos correlatos que detalham subtractive e nonsubtractive dither, incluindo provas de independência e resultados práticos. (collectionscanada.gc.ca)
  • Raspberry Pi. RP2040 Datasheet e documentação oficial (ADC, periféricos, Pico SDK). Utilize como referência de pinos, resolução e limites do ADC. (datasheets.raspberrypi.com, raspberrypi.com)
0 0 votos
Classificação do artigo
Inscrever-se
Notificar de
guest
0 Comentários
mais antigos
mais recentes Mais votado
Feedbacks embutidos
Ver todos os comentários

Related Post

Diferença entre Big Endian, Little Endian e Bit EndiannessDiferença entre Big Endian, Little Endian e Bit Endianness

25/07/202525/07/2025| Carlos DelfinoCarlos Delfino| 0 Comment| 09:51

Artigo originalmente postado em https://carlosdelfino.eti.br/programacao/cplusplus/Diferencas_entre_BigEndian_Little_Endian_e_Bit_Endianness/ Para iniciantes, este conceito pode parecer confuso e até inútil. No entanto, para quem deseja trabalhar com microcontroladores, processadores e, principalmente, redes a nível de

Read MoreRead More
0
Adoraria saber sua opinião, comente.x